Synthesis of Procedural Models for Deterministic Transition Systems

This paper introduces a general approach for synthesizing procedural models of the state-transitions of a given discrete system. The approach is general in that it accepts different target languages for modeling the state-transitions of a discrete system; different model acquisition tasks with different target languages, such as the synthesis of STRIPS action models, or the update rule of a cellular automaton, fit as particular instances of our general approach. We follow an inductive approach to synthesis meaning that a set of examples of state-transitions, represented as (pre-state, action, post-state) tuples, are given as input. The goal is to synthesize a structured program that, when executed on a given pre-state, outputs its associated post-state. Our synthesis method implements a combinatorial search in the space of well-structured terminating programs that can be built using a Random-Access Machine (RAM), with a minimalist instruction set, and a finite amount of memory. The combinatorial search is guided with functions that asses the complexity of the candidate programs, as well as their fitness to the given input set of examples.

Generalized Planning as Heuristic Search: A new planning search-space that leverages pointers over objects

Planning as heuristic search is one of the most successful approaches to classical planning but unfortunately, it does not extend trivially to Generalized Planning (GP). GP aims to compute algorithmic solutions that are valid for a set of classical planning instances from a given domain, even if these instances differ in the number of objects, the number of state variables, their domain size, or their initial and goal configuration. The generalization requirements of GP make it impractical to perform the state-space search that is usually implemented by heuristic planners. This paper adapts the planning as heuristic search paradigm to the generalization requirements of GP, and presents the first native heuristic search approach to GP. First, the paper introduces a new pointer-based solution space for GP that is independent of the number of classical planning instances in a GP problem and the size of those instances (i.e. the number of objects, state variables and their domain sizes). Second, the paper defines a set of evaluation and heuristic functions for guiding a combinatorial search in our new GP solution space. The computation of these evaluation and heuristic functions does not require grounding states or actions in advance. Therefore our GP as heuristic search approach can handle large sets of state variables with large numerical domains, e.g.~integers. Lastly, the paper defines an upgraded version of our novel algorithm for GP called Best-First Generalized Planning (BFGP), that implements a best-first search in our pointer-based solution space, and that is guided by our evaluation/heuristic functions for GP.

Representation and Synthesis of C++ Programs for Generalized Planning

The paper introduces a novel representation for Generalized Planning (GP) problems, and their solutions, as C++ programs. Our C++ representation allows to formally proving the termination of generalized plans, and to specifying their asymptotic complexity w.r.t. the number of world objects. Characterizing the complexity of C++ generalized plans enables the application of a combinatorial search that enumerates the space of possible GP solutions in order of complexity. Experimental results show that our implementation of this approach, which we call BFGP++, outperforms the previous GP as heuristic search approach for the computation of generalized plans represented as compiler-styled programs. Last but not least, the execution of a C++ program on a classical planning instance is a deterministic grounding-free and search-free process, so our C++ representation allows us to automatically validate the computed solutions on large test instances of thousands of objects, where off-the-shelf classical planners get stuck either in the pre-processing or in the search.

Computing Programs for Generalized Planning as Heuristic Search

Although heuristic search is one of the most successful approaches to classical planning, this planning paradigm does not apply straightforwardly to Generalized Planning (GP). This paper adapts the planning as heuristic search paradigm to the particularities of GP, and presents the first native heuristic search approach to GP. First, the paper defines a program-based solution space for GP that is independent of the number of planning instances in a GP problem, and the size of these instances. Second, the paper defines the BFGP algorithm for GP, that implements a best-first search in our program-based solution space, and that is guided by different evaluation and heuristic functions.

Scaling-up Generalized Planning as Heuristic Search with Landmarks

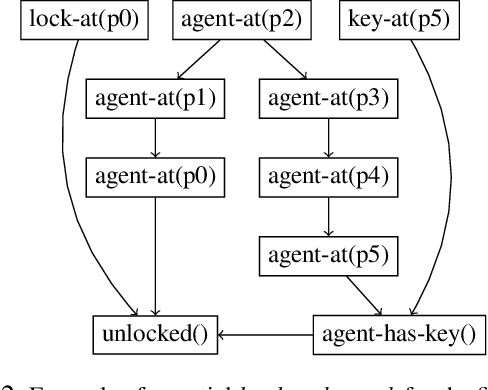
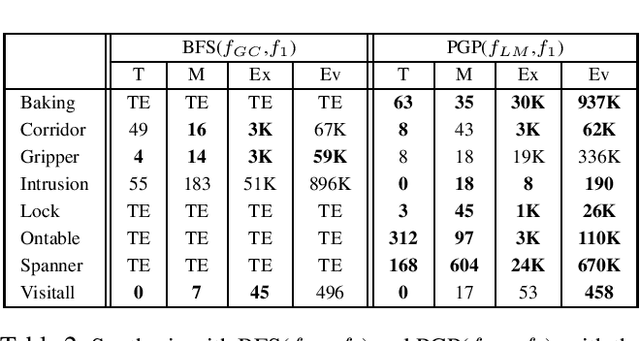
Landmarks are one of the most effective search heuristics for classical planning, but largely ignored in generalized planning. Generalized planning (GP) is usually addressed as a combinatorial search in a given space of algorithmic solutions, where candidate solutions are evaluated w.r.t.~the instances they solve. This type of solution evaluation ignores any sub-goal information that is not explicit in the representation of the planning instances, causing plateaus in the space of candidate generalized plans. Furthermore, node expansion in GP is a run-time bottleneck since it requires evaluating every child node over the entire batch of classical planning instances in a GP problem. In this paper we define a landmark counting heuristic for GP (that considers sub-goal information that is not explicitly represented in the planning instances), and a novel heuristic search algorithm for GP (that we call PGP) and that progressively processes subsets of the planning instances of a GP problem. Our two orthogonal contributions are analyzed in an ablation study, showing that both improve the state-of-the-art in GP as heuristic search, and that both benefit from each other when used in combination.

Generalized Planning as Heuristic Search

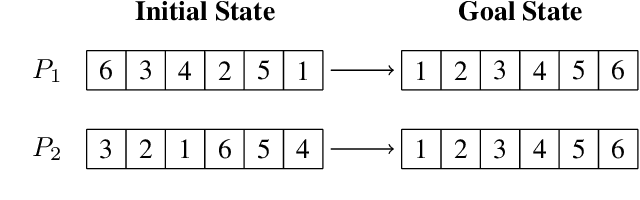
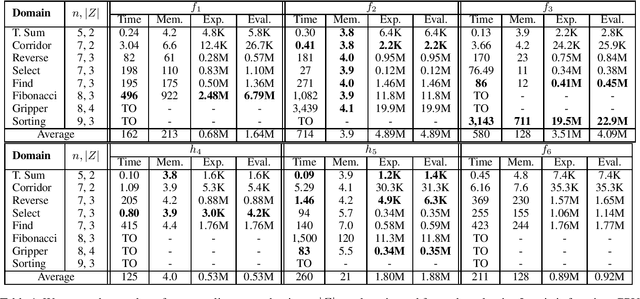
Although heuristic search is one of the most successful approaches to classical planning, this planning paradigm does not apply straightforwardly to Generalized Planning (GP). Planning as heuristic search traditionally addresses the computation of sequential plans by searching in a grounded state-space. On the other hand GP aims at computing algorithm-like plans, that can branch and loop, and that generalize to a (possibly infinite) set of classical planning instances. This paper adapts the planning as heuristic search paradigm to the particularities of GP, and presents the first native heuristic search approach to GP. First, the paper defines a novel GP solution space that is independent of the number of planning instances in a GP problem, and the size of these instances. Second, the paper defines different evaluation and heuristic functions for guiding a combinatorial search in our GP solution space. Lastly the paper defines a GP algorithm, called Best-First Generalized Planning (BFGP), that implements a best-first search in the solution space guided by our evaluation/heuristic functions.

Generalized Planning with Positive and Negative Examples

Generalized planning aims at computing an algorithm-like structure (generalized plan) that solves a set of multiple planning instances. In this paper we define negative examples for generalized planning as planning instances that must not be solved by a generalized plan. With this regard the paper extends the notion of validation of a generalized plan as the problem of verifying that a given generalized plan solves the set of input positives instances while it fails to solve a given input set of negative examples. This notion of plan validation allows us to define quantitative metrics to asses the generalization capacity of generalized plans. The paper also shows how to incorporate this new notion of plan validation into a compilation for plan synthesis that takes both positive and negative instances as input. Experiments show that incorporating negative examples can accelerate plan synthesis in several domains and leverage quantitative metrics to evaluate the generalization capacity of the synthesized plans.

Hierarchical Finite State Controllers for Generalized Planning

Finite State Controllers (FSCs) are an effective way to represent sequential plans compactly. By imposing appropriate conditions on transitions, FSCs can also represent generalized plans that solve a range of planning problems from a given domain. In this paper we introduce the concept of {\it hierarchical FSCs} for planning by allowing controllers to call other controllers. We show that hierarchical FSCs can represent generalized plans more compactly than individual FSCs. Moreover, our call mechanism makes it possible to generate hierarchical FSCs in a modular fashion, or even to apply recursion. We also introduce a compilation that enables a classical planner to generate hierarchical FSCs that solve challenging generalized planning problems. The compilation takes as input a set of planning problems from a given domain and outputs a single classical planning problem, whose solution corresponds to a hierarchical FSC.

Generalized Planning With Procedural Domain Control Knowledge

Generalized planning is the task of generating a single solution that is valid for a set of planning problems. In this paper we show how to represent and compute generalized plans using procedural Domain Control Knowledge (DCK). We define a {\it divide and conquer} approach that first generates the procedural DCK solving a set of planning problems representative of certain subtasks and then compile it as callable procedures of the overall generalized planning problem. Our procedure calling mechanism allows nested and recursive procedure calls and is implemented in PDDL so that classical planners can compute and exploit procedural DCK. Experiments show that an off-the-shelf classical planner, using procedural DCK as callable procedures, can compute generalized plans in a wide range of domains including non-trivial ones, such as sorting variable-size lists or DFS traversal of binary trees with variable size.

Learning STRIPS Action Models with Classical Planning

This paper presents a novel approach for learning STRIPS action models from examples that compiles this inductive learning task into a classical planning task. Interestingly, the compilation approach is flexible to different amounts of available input knowledge; the learning examples can range from a set of plans (with their corresponding initial and final states) to just a pair of initial and final states (no intermediate action or state is given). Moreover, the compilation accepts partially specified action models and it can be used to validate whether the observation of a plan execution follows a given STRIPS action model, even if this model is not fully specified.