Scaling-up Generalized Planning as Heuristic Search with Landmarks
Paper and Code
May 10, 2022

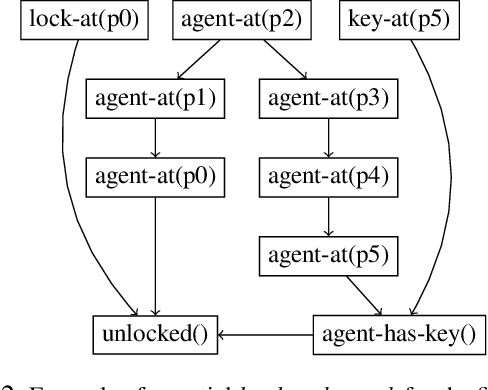
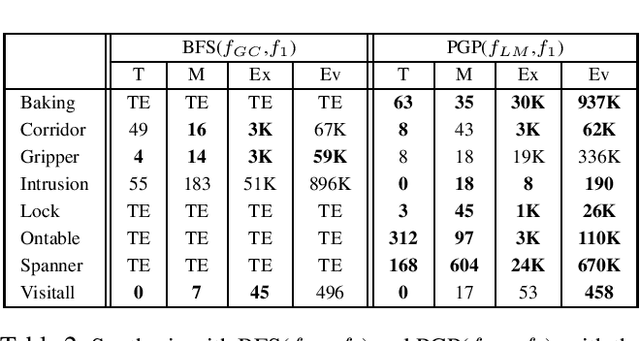
Landmarks are one of the most effective search heuristics for classical planning, but largely ignored in generalized planning. Generalized planning (GP) is usually addressed as a combinatorial search in a given space of algorithmic solutions, where candidate solutions are evaluated w.r.t.~the instances they solve. This type of solution evaluation ignores any sub-goal information that is not explicit in the representation of the planning instances, causing plateaus in the space of candidate generalized plans. Furthermore, node expansion in GP is a run-time bottleneck since it requires evaluating every child node over the entire batch of classical planning instances in a GP problem. In this paper we define a landmark counting heuristic for GP (that considers sub-goal information that is not explicitly represented in the planning instances), and a novel heuristic search algorithm for GP (that we call PGP) and that progressively processes subsets of the planning instances of a GP problem. Our two orthogonal contributions are analyzed in an ablation study, showing that both improve the state-of-the-art in GP as heuristic search, and that both benefit from each other when used in combination.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge