Laura Sebastiá
Scaling-up Generalized Planning as Heuristic Search with Landmarks
May 10, 2022

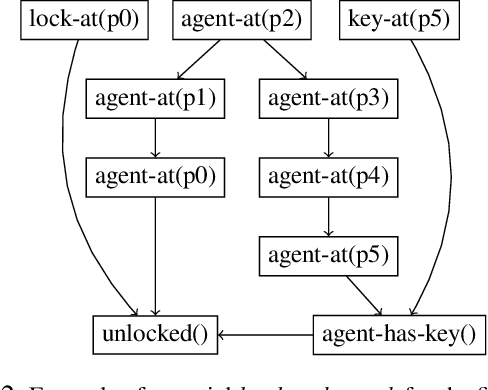
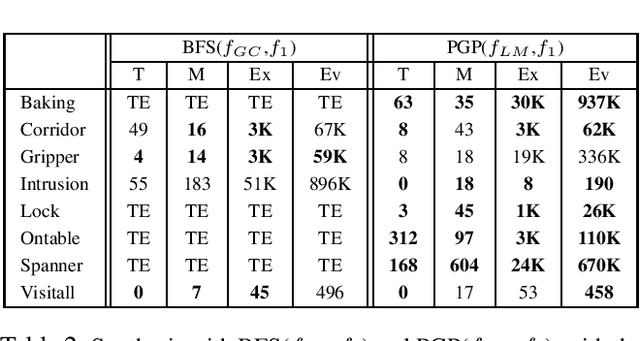
Abstract:Landmarks are one of the most effective search heuristics for classical planning, but largely ignored in generalized planning. Generalized planning (GP) is usually addressed as a combinatorial search in a given space of algorithmic solutions, where candidate solutions are evaluated w.r.t.~the instances they solve. This type of solution evaluation ignores any sub-goal information that is not explicit in the representation of the planning instances, causing plateaus in the space of candidate generalized plans. Furthermore, node expansion in GP is a run-time bottleneck since it requires evaluating every child node over the entire batch of classical planning instances in a GP problem. In this paper we define a landmark counting heuristic for GP (that considers sub-goal information that is not explicitly represented in the planning instances), and a novel heuristic search algorithm for GP (that we call PGP) and that progressively processes subsets of the planning instances of a GP problem. Our two orthogonal contributions are analyzed in an ablation study, showing that both improve the state-of-the-art in GP as heuristic search, and that both benefit from each other when used in combination.
Evaluating the quality of tourist agendas customized to different travel styles
Jun 17, 2017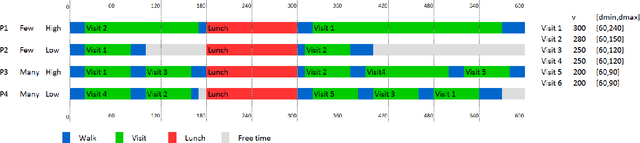
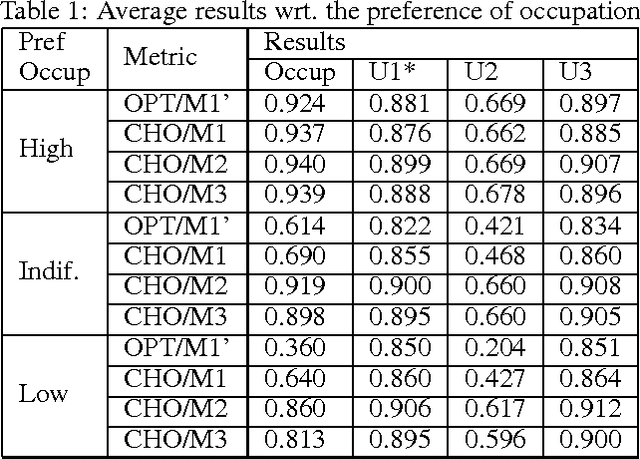

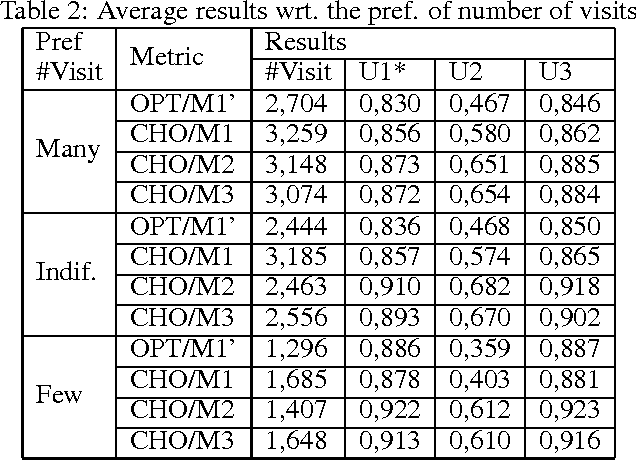
Abstract:Many tourist applications provide a personalized tourist agenda with the list of recommended activities to the user. These applications must undoubtedly deal with the constraints and preferences that define the user interests. Among these preferences, we can find those that define the travel style of the user, such as the rhythm of the trip, the number of visits to include in the tour or the priority to visits of special interest for the user. In this paper, we deal with the task of creating a customized tourist agenda as a planning and scheduling application capable of conveniently scheduling the most appropriate goals (visits) so as to maximize the user satisfaction with the tourist route. This paper makes an analysis of the meaning of the travel style preferences and compares the quality of the solutions obtained by two different solvers, a PDDL-based planner and a Constraint Satisfaction Problem solver. We also define several quality metrics and perform extensive experiments in order to evaluate the results obtained with both solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge