Subgoaling Relaxation-based Heuristics for Numeric Planning with Infinite Actions

Numeric planning with control parameters extends the standard numeric planning model by introducing action parameters as free numeric variables that must be instantiated during planning. This results in a potentially infinite number of applicable actions in a state. In this setting, off-the-shelf numeric heuristics that leverage the action structure are not feasible. In this paper, we identify a tractable subset of these problems--namely, controllable, simple numeric problems--and propose an optimistic compilation approach that transforms them into simple numeric tasks. To do so, we abstract control-dependent expressions into bounded constant effects and relaxed preconditions. The proposed compilation makes it possible to effectively use subgoaling heuristics to estimate goal distance in numeric planning problems involving control parameters. Our results demonstrate that this approach is an effective and computationally feasible way of applying traditional numeric heuristics to settings with an infinite number of possible actions, pushing the boundaries of the current state of the art.

Handling Infinite Domain Parameters in Planning Through Best-First Search with Delayed Partial Expansions

In automated planning, control parameters extend standard action representations through the introduction of continuous numeric decision variables. Existing state-of-the-art approaches have primarily handled control parameters as embedded constraints alongside other temporal and numeric restrictions, and thus have implicitly treated them as additional constraints rather than as decision points in the search space. In this paper, we propose an efficient alternative that explicitly handles control parameters as true decision points within a systematic search scheme. We develop a best-first, heuristic search algorithm that operates over infinite decision spaces defined by control parameters and prove a notion of completeness in the limit under certain conditions. Our algorithm leverages the concept of delayed partial expansion, where a state is not fully expanded but instead incrementally expands a subset of its successors. Our results demonstrate that this novel search algorithm is a competitive alternative to existing approaches for solving planning problems involving control parameters.

Action Model Learning with Guarantees

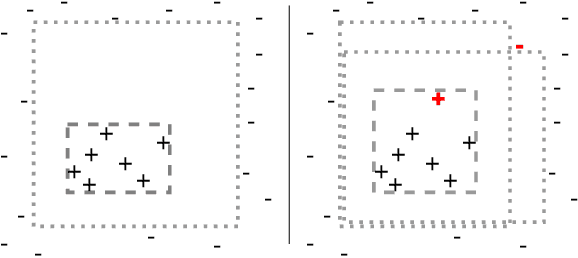
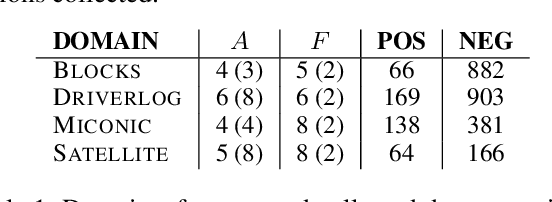
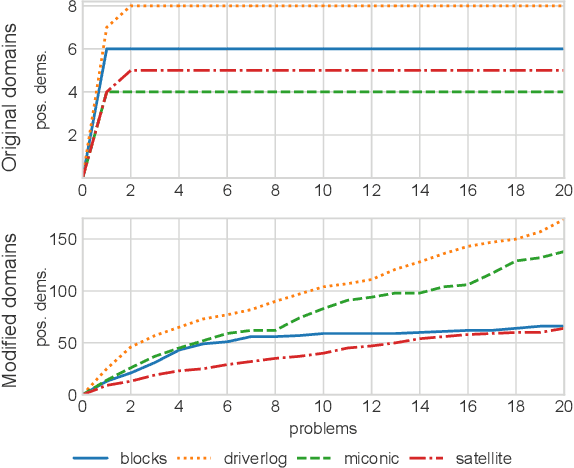
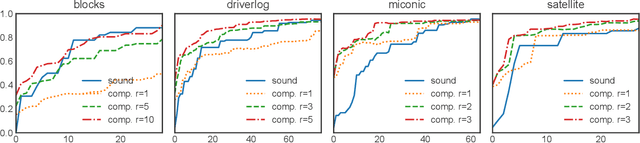
This paper studies the problem of action model learning with full observability. Following the learning by search paradigm by Mitchell, we develop a theory for action model learning based on version spaces that interprets the task as search for hypothesis that are consistent with the learning examples. Our theoretical findings are instantiated in an online algorithm that maintains a compact representation of all solutions of the problem. Among these range of solutions, we bring attention to actions models approximating the actual transition system from below (sound models) and from above (complete models). We show how to manipulate the output of our learning algorithm to build deterministic and non-deterministic formulations of the sound and complete models and prove that, given enough examples, both formulations converge into the very same true model. Our experiments reveal their usefulness over a range of planning domains.

Learning STRIPS Action Models with Classical Planning

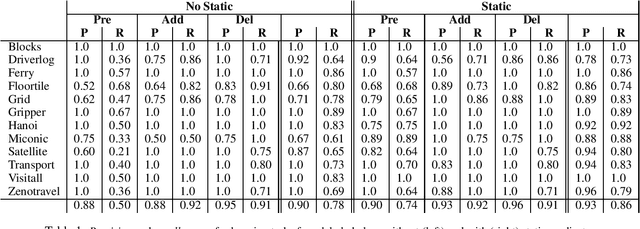
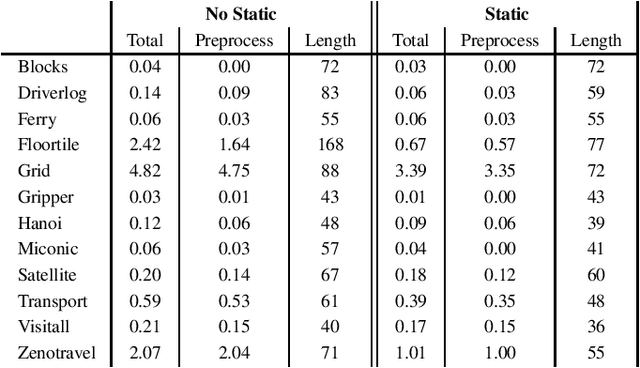
This paper presents a novel approach for learning STRIPS action models from examples that compiles this inductive learning task into a classical planning task. Interestingly, the compilation approach is flexible to different amounts of available input knowledge; the learning examples can range from a set of plans (with their corresponding initial and final states) to just a pair of initial and final states (no intermediate action or state is given). Moreover, the compilation accepts partially specified action models and it can be used to validate whether the observation of a plan execution follows a given STRIPS action model, even if this model is not fully specified.