Subgoaling Relaxation-based Heuristics for Numeric Planning with Infinite Actions

Numeric planning with control parameters extends the standard numeric planning model by introducing action parameters as free numeric variables that must be instantiated during planning. This results in a potentially infinite number of applicable actions in a state. In this setting, off-the-shelf numeric heuristics that leverage the action structure are not feasible. In this paper, we identify a tractable subset of these problems--namely, controllable, simple numeric problems--and propose an optimistic compilation approach that transforms them into simple numeric tasks. To do so, we abstract control-dependent expressions into bounded constant effects and relaxed preconditions. The proposed compilation makes it possible to effectively use subgoaling heuristics to estimate goal distance in numeric planning problems involving control parameters. Our results demonstrate that this approach is an effective and computationally feasible way of applying traditional numeric heuristics to settings with an infinite number of possible actions, pushing the boundaries of the current state of the art.

Two Constraint Compilation Methods for Lifted Planning

We study planning in a fragment of PDDL with qualitative state-trajectory constraints, capturing safety requirements, task ordering conditions, and intermediate sub-goals commonly found in real-world problems. A prominent approach to tackle such problems is to compile their constraints away, leading to a problem that is supported by state-of-the-art planners. Unfortunately, existing compilers do not scale on problems with a large number of objects and high-arity actions, as they necessitate grounding the problem before compilation. To address this issue, we propose two methods for compiling away constraints without grounding, making them suitable for large-scale planning problems. We prove the correctness of our compilers and outline their worst-case time complexity. Moreover, we present a reproducible empirical evaluation on the domains used in the latest International Planning Competition. Our results demonstrate that our methods are efficient and produce planning specifications that are orders of magnitude more succinct than the ones produced by compilers that ground the domain, while remaining competitive when used for planning with a state-of-the-art planner.

Handling Infinite Domain Parameters in Planning Through Best-First Search with Delayed Partial Expansions

In automated planning, control parameters extend standard action representations through the introduction of continuous numeric decision variables. Existing state-of-the-art approaches have primarily handled control parameters as embedded constraints alongside other temporal and numeric restrictions, and thus have implicitly treated them as additional constraints rather than as decision points in the search space. In this paper, we propose an efficient alternative that explicitly handles control parameters as true decision points within a systematic search scheme. We develop a best-first, heuristic search algorithm that operates over infinite decision spaces defined by control parameters and prove a notion of completeness in the limit under certain conditions. Our algorithm leverages the concept of delayed partial expansion, where a state is not fully expanded but instead incrementally expands a subset of its successors. Our results demonstrate that this novel search algorithm is a competitive alternative to existing approaches for solving planning problems involving control parameters.

Action Model Learning with Guarantees

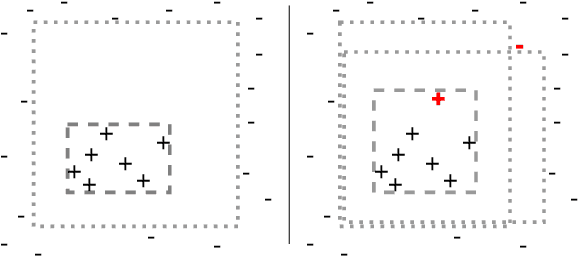
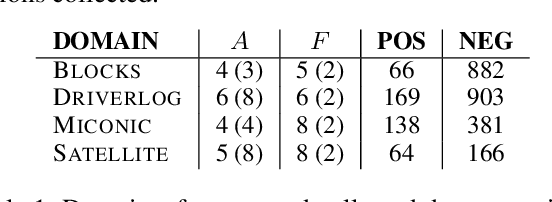
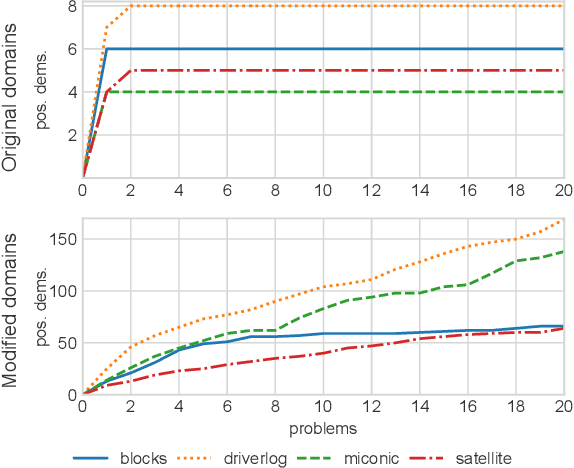
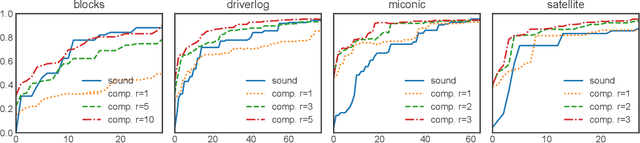
This paper studies the problem of action model learning with full observability. Following the learning by search paradigm by Mitchell, we develop a theory for action model learning based on version spaces that interprets the task as search for hypothesis that are consistent with the learning examples. Our theoretical findings are instantiated in an online algorithm that maintains a compact representation of all solutions of the problem. Among these range of solutions, we bring attention to actions models approximating the actual transition system from below (sound models) and from above (complete models). We show how to manipulate the output of our learning algorithm to build deterministic and non-deterministic formulations of the sound and complete models and prove that, given enough examples, both formulations converge into the very same true model. Our experiments reveal their usefulness over a range of planning domains.

Safe Learning of PDDL Domains with Conditional Effects -- Extended Version

Powerful domain-independent planners have been developed to solve various types of planning problems. These planners often require a model of the acting agent's actions, given in some planning domain description language. Manually designing such an action model is a notoriously challenging task. An alternative is to automatically learn action models from observation. Such an action model is called safe if every plan created with it is consistent with the real, unknown action model. Algorithms for learning such safe action models exist, yet they cannot handle domains with conditional or universal effects, which are common constructs in many planning problems. We prove that learning non-trivial safe action models with conditional effects may require an exponential number of samples. Then, we identify reasonable assumptions under which such learning is tractable and propose SAM Learning of Conditional Effects (Conditional-SAM), the first algorithm capable of doing so. We analyze Conditional-SAM theoretically and evaluate it experimentally. Our results show that the action models learned by Conditional-SAM can be used to solve perfectly most of the test set problems in most of the experimented domains.

Numerical Integration and Dynamic Discretization in Heuristic Search Planning over Hybrid Domains

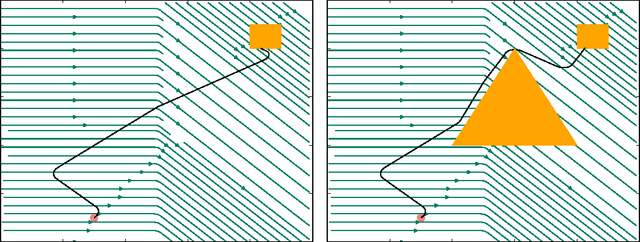
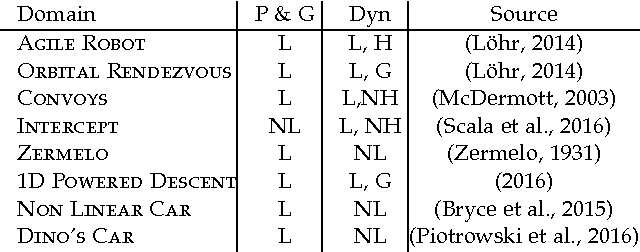
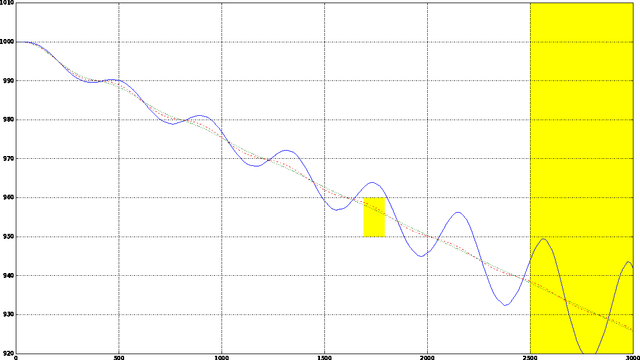
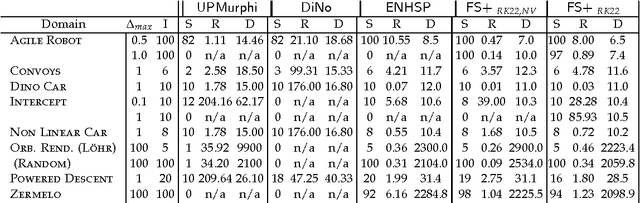
In this paper we look into the problem of planning over hybrid domains, where change can be both discrete and instantaneous, or continuous over time. In addition, it is required that each state on the trajectory induced by the execution of plans complies with a given set of global constraints. We approach the computation of plans for such domains as the problem of searching over a deterministic state model. In this model, some of the successor states are obtained by solving numerically the so-called initial value problem over a set of ordinary differential equations (ODE) given by the current plan prefix. These equations hold over time intervals whose duration is determined dynamically, according to whether zero crossing events take place for a set of invariant conditions. The resulting planner, FS+, incorporates these features together with effective heuristic guidance. FS+ does not impose any of the syntactic restrictions on process effects often found on the existing literature on Hybrid Planning. A key concept of our approach is that a clear separation is struck between planning and simulation time steps. The former is the time allowed to observe the evolution of a given dynamical system before committing to a future course of action, whilst the later is part of the model of the environment. FS+ is shown to be a robust planner over a diverse set of hybrid domains, taken from the existing literature on hybrid planning and systems.