Numerical Integration and Dynamic Discretization in Heuristic Search Planning over Hybrid Domains
Paper and Code
Mar 13, 2017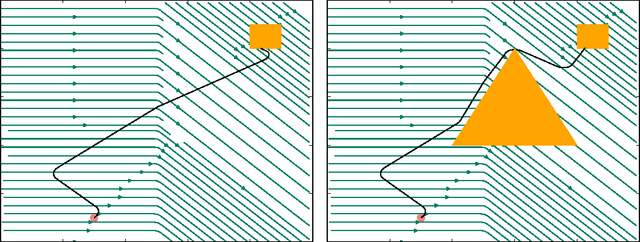
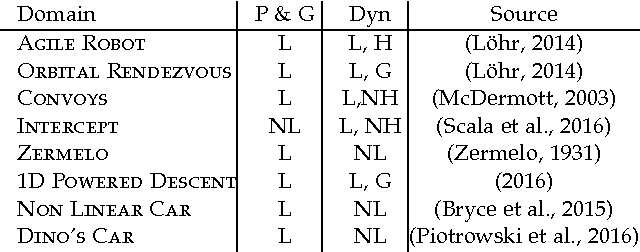
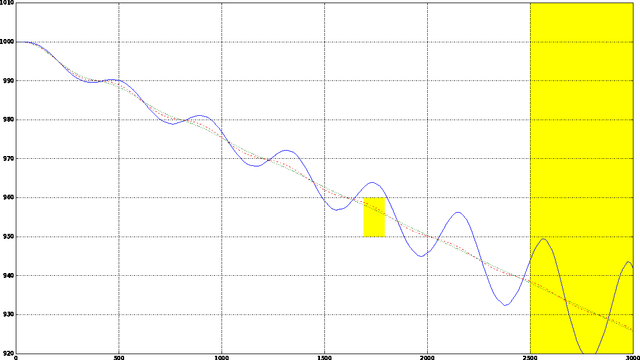
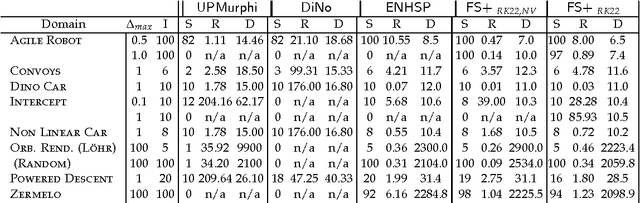
In this paper we look into the problem of planning over hybrid domains, where change can be both discrete and instantaneous, or continuous over time. In addition, it is required that each state on the trajectory induced by the execution of plans complies with a given set of global constraints. We approach the computation of plans for such domains as the problem of searching over a deterministic state model. In this model, some of the successor states are obtained by solving numerically the so-called initial value problem over a set of ordinary differential equations (ODE) given by the current plan prefix. These equations hold over time intervals whose duration is determined dynamically, according to whether zero crossing events take place for a set of invariant conditions. The resulting planner, FS+, incorporates these features together with effective heuristic guidance. FS+ does not impose any of the syntactic restrictions on process effects often found on the existing literature on Hybrid Planning. A key concept of our approach is that a clear separation is struck between planning and simulation time steps. The former is the time allowed to observe the evolution of a given dynamical system before committing to a future course of action, whilst the later is part of the model of the environment. FS+ is shown to be a robust planner over a diverse set of hybrid domains, taken from the existing literature on hybrid planning and systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge