Sylvie Thiebaux
Learning Efficiency Meets Symmetry Breaking
Apr 28, 2025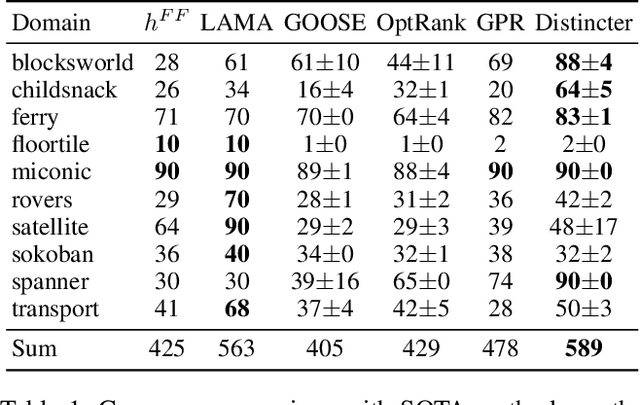
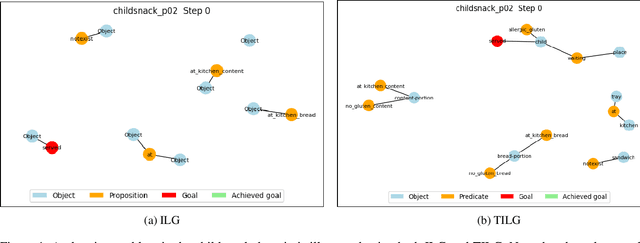
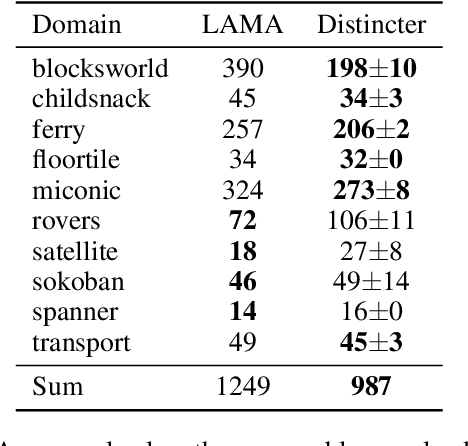
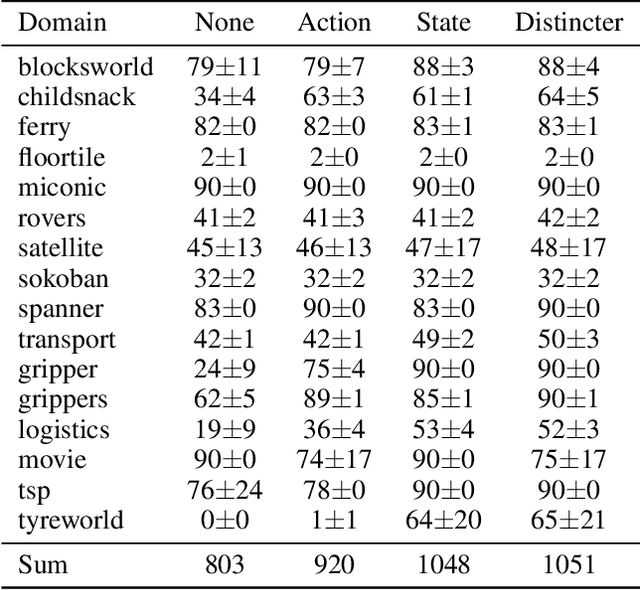
Abstract:Learning-based planners leveraging Graph Neural Networks can learn search guidance applicable to large search spaces, yet their potential to address symmetries remains largely unexplored. In this paper, we introduce a graph representation of planning problems allying learning efficiency with the ability to detect symmetries, along with two pruning methods, action pruning and state pruning, designed to manage symmetries during search. The integration of these techniques into Fast Downward achieves a first-time success over LAMA on the latest IPC learning track dataset. Code is released at: https://github.com/bybeye/Distincter.
Decision-Focused Learning to Predict Action Costs for Planning
Aug 13, 2024

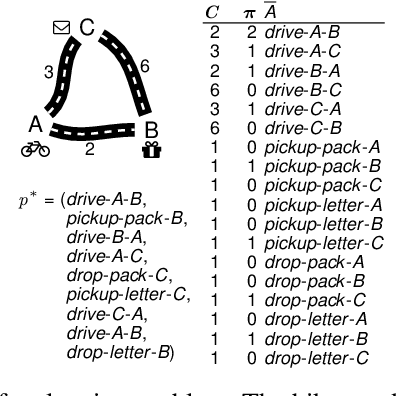

Abstract:In many automated planning applications, action costs can be hard to specify. An example is the time needed to travel through a certain road segment, which depends on many factors, such as the current weather conditions. A natural way to address this issue is to learn to predict these parameters based on input features (e.g., weather forecasts) and use the predicted action costs in automated planning afterward. Decision-Focused Learning (DFL) has been successful in learning to predict the parameters of combinatorial optimization problems in a way that optimizes solution quality rather than prediction quality. This approach yields better results than treating prediction and optimization as separate tasks. In this paper, we investigate for the first time the challenges of implementing DFL for automated planning in order to learn to predict the action costs. There are two main challenges to overcome: (1) planning systems are called during gradient descent learning, to solve planning problems with negative action costs, which are not supported in planning. We propose novel methods for gradient computation to avoid this issue. (2) DFL requires repeated planner calls during training, which can limit the scalability of the method. We experiment with different methods approximating the optimal plan as well as an easy-to-implement caching mechanism to speed up the learning process. As the first work that addresses DFL for automated planning, we demonstrate that the proposed gradient computation consistently yields significantly better plans than predictions aimed at minimizing prediction error; and that caching can temper the computation requirements.
Numerical Integration and Dynamic Discretization in Heuristic Search Planning over Hybrid Domains
Mar 13, 2017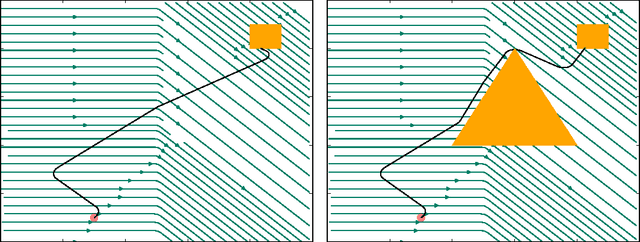
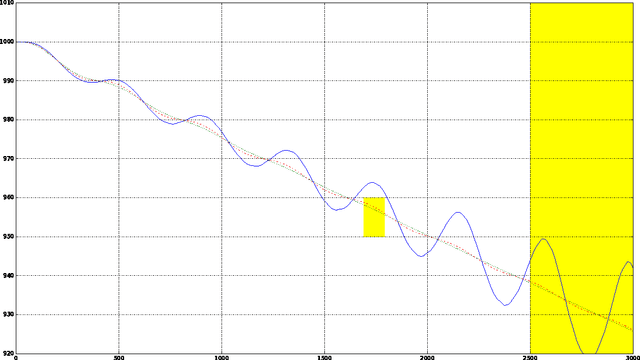
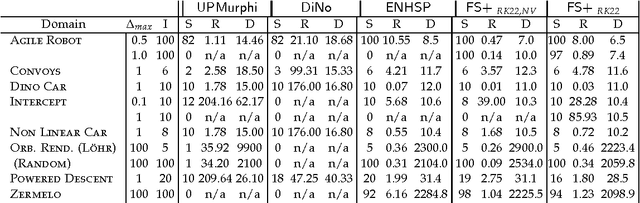
Abstract:In this paper we look into the problem of planning over hybrid domains, where change can be both discrete and instantaneous, or continuous over time. In addition, it is required that each state on the trajectory induced by the execution of plans complies with a given set of global constraints. We approach the computation of plans for such domains as the problem of searching over a deterministic state model. In this model, some of the successor states are obtained by solving numerically the so-called initial value problem over a set of ordinary differential equations (ODE) given by the current plan prefix. These equations hold over time intervals whose duration is determined dynamically, according to whether zero crossing events take place for a set of invariant conditions. The resulting planner, FS+, incorporates these features together with effective heuristic guidance. FS+ does not impose any of the syntactic restrictions on process effects often found on the existing literature on Hybrid Planning. A key concept of our approach is that a clear separation is struck between planning and simulation time steps. The former is the time allowed to observe the evolution of a given dynamical system before committing to a future course of action, whilst the later is part of the model of the environment. FS+ is shown to be a robust planner over a diverse set of hybrid domains, taken from the existing literature on hybrid planning and systems.
Supply Restoration in Power Distribution Systems - A Case Study in Integrating Model-Based Diagnosis and Repair Planning
Feb 13, 2013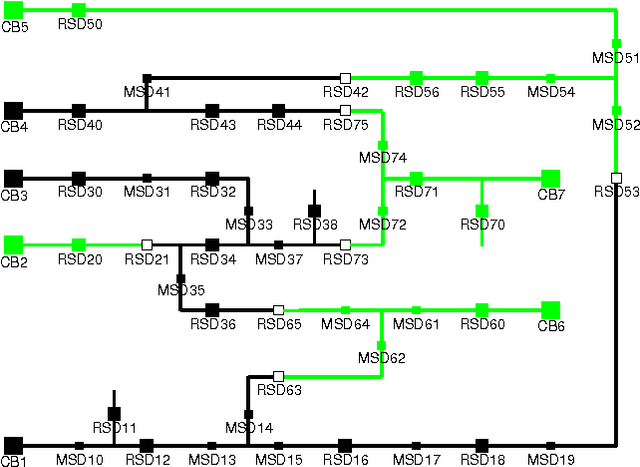


Abstract:Integrating diagnosis and repair is particularly crucial when gaining sufficient information to discriminate between several candidate diagnoses requires carrying out some repair actions. A typical case is supply restoration in a faulty power distribution system. This problem, which is a major concern for electricity distributors, features partial observability, and stochastic repair actions which are more elaborate than simple replacement of components. This paper analyses the difficulties in applying existing work on integrating model-based diagnosis and repair and on planning in partially observable stochastic domains to this real-world problem, and describes the pragmatic approach we have retained so far.
Anytime State-Based Solution Methods for Decision Processes with non-Markovian Rewards
Dec 12, 2012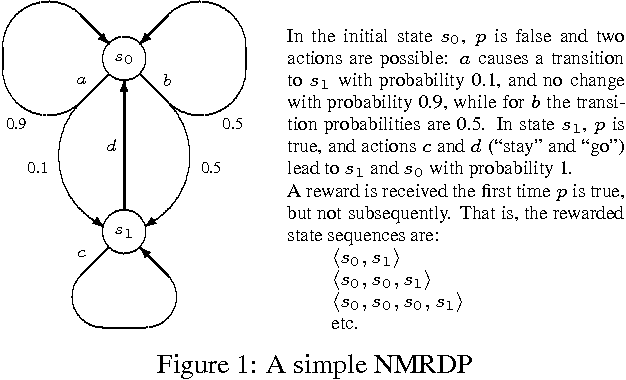
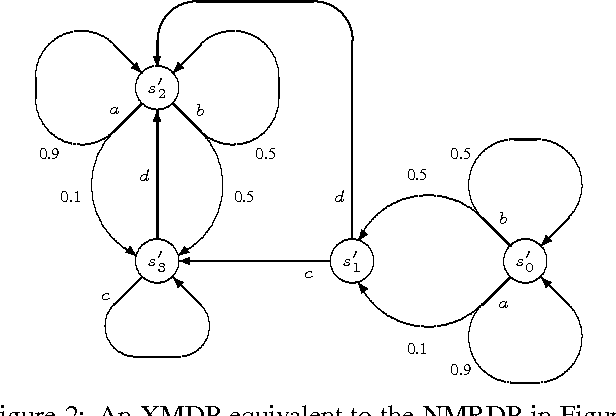
Abstract:A popular approach to solving a decision process with non-Markovian rewards (NMRDP) is to exploit a compact representation of the reward function to automatically translate the NMRDP into an equivalent Markov decision process (MDP) amenable to our favorite MDP solution method. The contribution of this paper is a representation of non-Markovian reward functions and a translation into MDP aimed at making the best possible use of state-based anytime algorithms as the solution method. By explicitly constructing and exploring only parts of the state space, these algorithms are able to trade computation time for policy quality, and have proven quite effective in dealing with large MDPs. Our representation extends future linear temporal logic (FLTL) to express rewards. Our translation has the effect of embedding model-checking in the solution method. It results in an MDP of the minimal size achievable without stepping outside the anytime framework, and consequently in better policies by the deadline.
Implementation and Comparison of Solution Methods for Decision Processes with Non-Markovian Rewards
Oct 19, 2012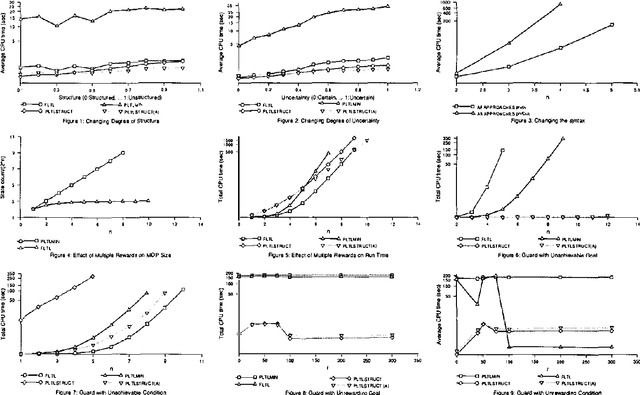

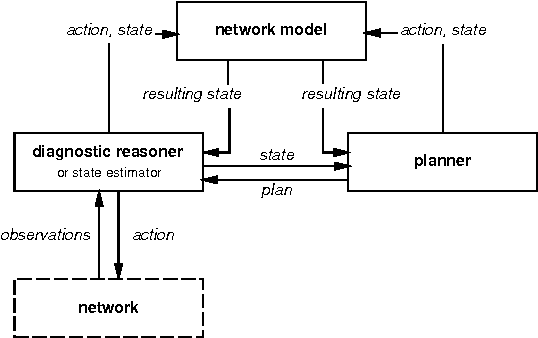
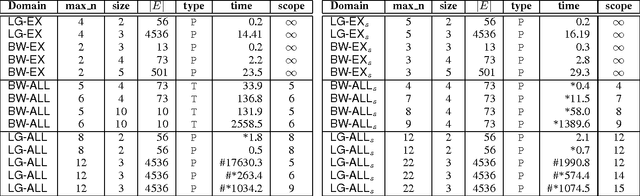
Abstract:This paper examines a number of solution methods for decision processes with non-Markovian rewards (NMRDPs). They all exploit a temporal logic specification of the reward function to automatically translate the NMRDP into an equivalent Markov decision process (MDP) amenable to well-known MDP solution methods. They differ however in the representation of the target MDP and the class of MDP solution methods to which they are suited. As a result, they adopt different temporal logics and different translations. Unfortunately, no implementation of these methods nor experimental let alone comparative results have ever been reported. This paper is the first step towards filling this gap. We describe an integrated system for solving NMRDPs which implements these methods and several variants under a common interface; we use it to compare the various approaches and identify the problem features favoring one over the other.
Exploiting First-Order Regression in Inductive Policy Selection
Jul 11, 2012
Abstract:We consider the problem of computing optimal generalised policies for relational Markov decision processes. We describe an approach combining some of the benefits of purely inductive techniques with those of symbolic dynamic programming methods. The latter reason about the optimal value function using first-order decision theoretic regression and formula rewriting, while the former, when provided with a suitable hypotheses language, are capable of generalising value functions or policies for small instances. Our idea is to use reasoning and in particular classical first-order regression to automatically generate a hypotheses language dedicated to the domain at hand, which is then used as input by an inductive solver. This approach avoids the more complex reasoning of symbolic dynamic programming while focusing the inductive solver's attention on concepts that are specifically relevant to the optimal value function for the domain considered.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge