Jayanta Mandi
Feasibility-Aware Decision-Focused Learning for Predicting Parameters in the Constraints
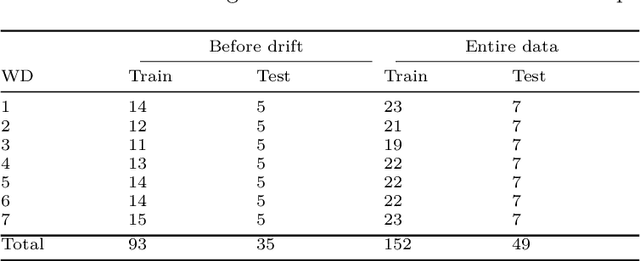
Oct 06, 2025Abstract:When some parameters of a constrained optimization problem (COP) are uncertain, this gives rise to a predict-then-optimize (PtO) problem, comprising two stages -- the prediction of the unknown parameters from contextual information and the subsequent optimization using those predicted parameters. Decision-focused learning (DFL) implements the first stage by training a machine learning (ML) model to optimize the quality of the decisions made using the predicted parameters. When parameters in the constraints of a COP are predicted, the predicted parameters can lead to infeasible solutions. Therefore, it is important to simultaneously manage both feasibility and decision quality. We develop a DFL framework for predicting constraint parameters in a generic COP. While prior works typically assume that the underlying optimization problem is a linear program (LP) or integer linear program (ILP), our approach makes no such assumption. We derive two novel loss functions based on maximum likelihood estimation (MLE): the first one penalizes infeasibility (by penalizing when the predicted parameters lead to infeasible solutions), and the second one penalizes suboptimal decisions (by penalizing when the true optimal solution is infeasible under the predicted parameters). We introduce a single tunable parameter to form a weighted average of the two losses, allowing decision-makers to balance suboptimality and feasibility. We experimentally demonstrate that adjusting this parameter provides a decision-maker the control over the trade-off between the two. Moreover, across several COP instances, we find that for a single value of the tunable parameter, our method matches the performance of the existing baselines on suboptimality and feasibility.
Preference Elicitation for Multi-objective Combinatorial Optimization with Active Learning and Maximum Likelihood Estimation
Mar 14, 2025Abstract:Real-life combinatorial optimization problems often involve several conflicting objectives, such as price, product quality and sustainability. A computationally-efficient way to tackle multiple objectives is to aggregate them into a single-objective function, such as a linear combination. However, defining the weights of the linear combination upfront is hard; alternatively, the use of interactive learning methods that ask users to compare candidate solutions is highly promising. The key challenges are to generate candidates quickly, to learn an objective function that leads to high-quality solutions and to do so with few user interactions. We build upon the Constructive Preference Elicitation framework and show how each of the three properties can be improved: to increase the interaction speed we investigate using pools of (relaxed) solutions, to improve the learning we adopt Maximum Likelihood Estimation of a Bradley-Terry preference model; and to reduce the number of user interactions, we select the pair of candidates to compare with an ensemble-based acquisition function inspired from Active Learning. Our careful experimentation demonstrates each of these improvements: on a PC configuration task and a realistic multi-instance routing problem, our method selects queries faster, needs fewer queries and synthesizes higher-quality combinatorial solutions than previous CPE methods.
Decision-Focused Learning to Predict Action Costs for Planning
Aug 13, 2024

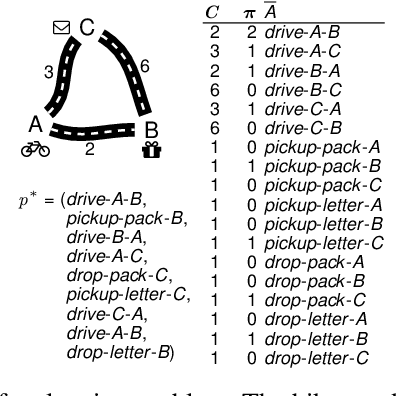

Abstract:In many automated planning applications, action costs can be hard to specify. An example is the time needed to travel through a certain road segment, which depends on many factors, such as the current weather conditions. A natural way to address this issue is to learn to predict these parameters based on input features (e.g., weather forecasts) and use the predicted action costs in automated planning afterward. Decision-Focused Learning (DFL) has been successful in learning to predict the parameters of combinatorial optimization problems in a way that optimizes solution quality rather than prediction quality. This approach yields better results than treating prediction and optimization as separate tasks. In this paper, we investigate for the first time the challenges of implementing DFL for automated planning in order to learn to predict the action costs. There are two main challenges to overcome: (1) planning systems are called during gradient descent learning, to solve planning problems with negative action costs, which are not supported in planning. We propose novel methods for gradient computation to avoid this issue. (2) DFL requires repeated planner calls during training, which can limit the scalability of the method. We experiment with different methods approximating the optimal plan as well as an easy-to-implement caching mechanism to speed up the learning process. As the first work that addresses DFL for automated planning, we demonstrate that the proposed gradient computation consistently yields significantly better plans than predictions aimed at minimizing prediction error; and that caching can temper the computation requirements.
Decision-Focused Learning: Foundations, State of the Art, Benchmark and Future Opportunities
Aug 16, 2023



Abstract:Decision-focused learning (DFL) is an emerging paradigm in machine learning which trains a model to optimize decisions, integrating prediction and optimization in an end-to-end system. This paradigm holds the promise to revolutionize decision-making in many real-world applications which operate under uncertainty, where the estimation of unknown parameters within these decision models often becomes a substantial roadblock. This paper presents a comprehensive review of DFL. It provides an in-depth analysis of the various techniques devised to integrate machine learning and optimization models, introduces a taxonomy of DFL methods distinguished by their unique characteristics, and conducts an extensive empirical evaluation of these methods proposing suitable benchmark dataset and tasks for DFL. Finally, the study provides valuable insights into current and potential future avenues in DFL research.
Score Function Gradient Estimation to Widen the Applicability of Decision-Focused Learning
Jul 11, 2023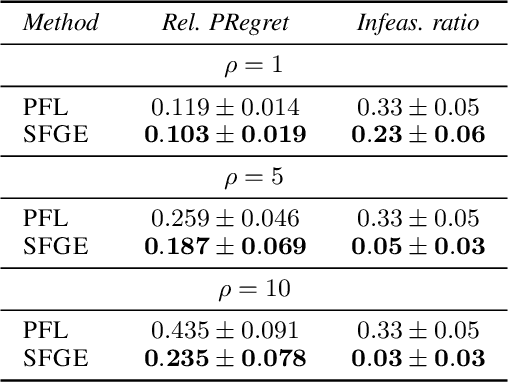
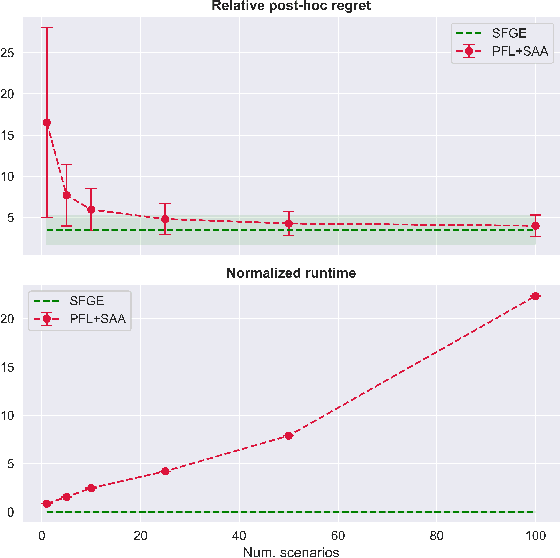
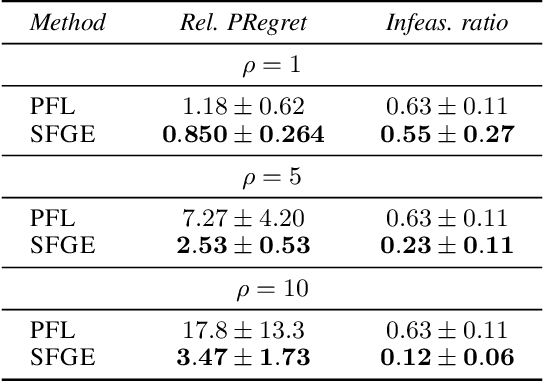
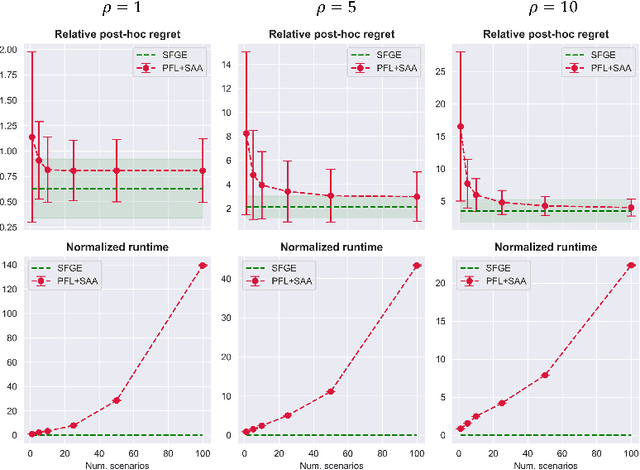
Abstract:Many real-world optimization problems contain unknown parameters that must be predicted prior to solving. To train the predictive machine learning (ML) models involved, the commonly adopted approach focuses on maximizing predictive accuracy. However, this approach does not always lead to the minimization of the downstream task loss. Decision-focused learning (DFL) is a recently proposed paradigm whose goal is to train the ML model by directly minimizing the task loss. However, state-of-the-art DFL methods are limited by the assumptions they make about the structure of the optimization problem (e.g., that the problem is linear) and by the fact that can only predict parameters that appear in the objective function. In this work, we address these limitations by instead predicting \textit{distributions} over parameters and adopting score function gradient estimation (SFGE) to compute decision-focused updates to the predictive model, thereby widening the applicability of DFL. Our experiments show that by using SFGE we can: (1) deal with predictions that occur both in the objective function and in the constraints; and (2) effectively tackle two-stage stochastic optimization problems.
Probability estimation and structured output prediction for learning preferences in last mile delivery
Jan 25, 2022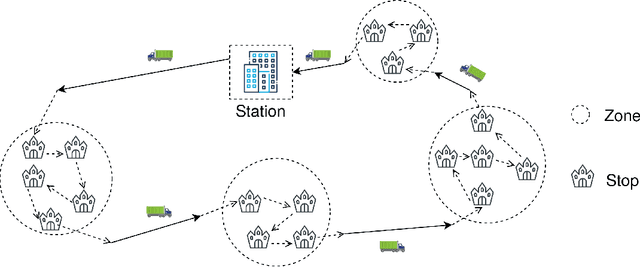
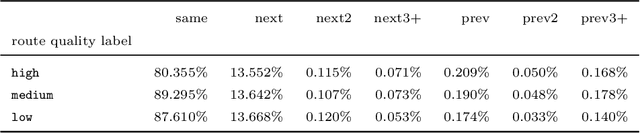
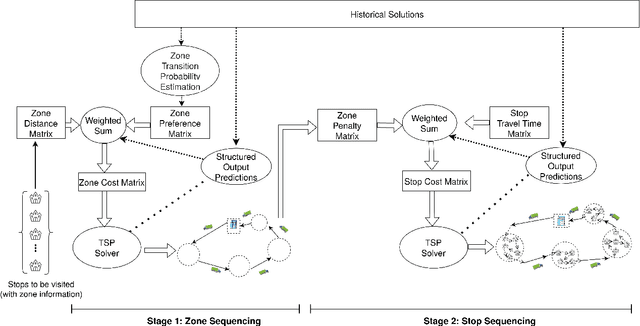
Abstract:We study the problem of learning the preferences of drivers and planners in the context of last mile delivery. Given a data set containing historical decisions and delivery locations, the goal is to capture the implicit preferences of the decision-makers. We consider two ways to use the historical data: one is through a probability estimation method that learns transition probabilities between stops (or zones). This is a fast and accurate method, recently studied in a VRP setting. Furthermore, we explore the use of machine learning to infer how to best balance multiple objectives such as distance, probability and penalties. Specifically, we cast the learning problem as a structured output prediction problem, where training is done by repeatedly calling the TSP solver. Another important aspect we consider is that for last-mile delivery, every address is a potential client and hence the data is very sparse. Hence, we propose a two-stage approach that first learns preferences at the zone level in order to compute a zone routing; after which a penalty-based TSP computes the stop routing. Results show that the zone transition probability estimation performs well, and that the structured output prediction learning can improve the results further. We hence showcase a successful combination of both probability estimation and machine learning, all the while using standard TSP solvers, both during learning and to compute the final solution; this means the methodology is applicable to other, real-life, TSP variants, or proprietary solvers.
Predict and Optimize: Through the Lens of Learning to Rank
Dec 07, 2021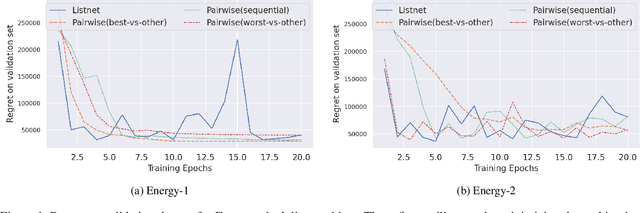
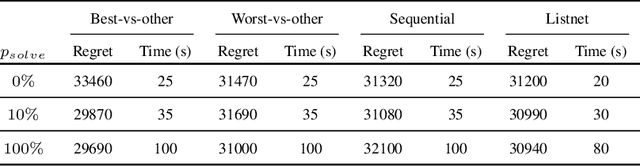
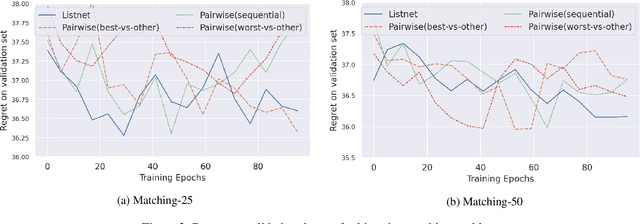

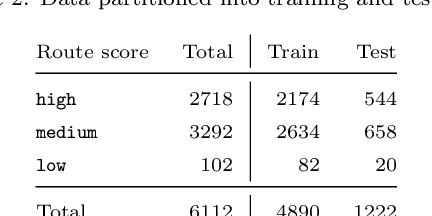
Abstract:In the last years predict-and-optimize approaches (Elmachtoub and Grigas 2021; Wilder, Dilkina, and Tambe 2019) have received increasing attention. These problems have the settings where the predictions of predictive machine learning (ML) models are fed to downstream optimization problems for decision making. Predict-and-optimize approaches propose to train the ML models, often neural network models, by directly optimizing the quality of decisions made by the optimization solvers. However, one major bottleneck of predict-and-optimize approaches is solving the optimization problem for each training instance at every epoch. To address this challenge, Mulamba et al. (2021) propose noise contrastive estimation by caching feasible solutions. In this work, we show the noise contrastive estimation can be considered a case of learning to rank the solution cache. We also develop pairwise and listwise ranking loss functions, which can be differentiated in closed form without the need of solving the optimization problem. By training with respect to these surrogate loss function, we empirically show that we are able to minimize the regret of the predictions.
Data Driven VRP: A Neural Network Model to Learn Hidden Preferences for VRP
Aug 27, 2021
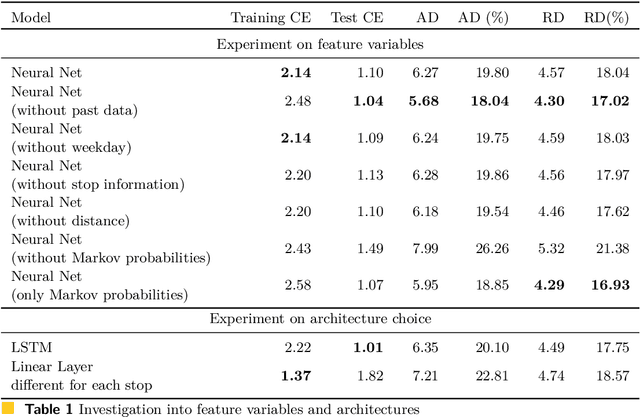
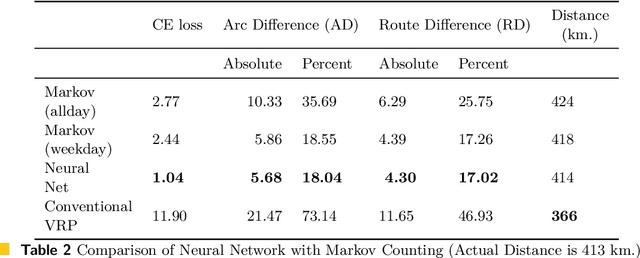
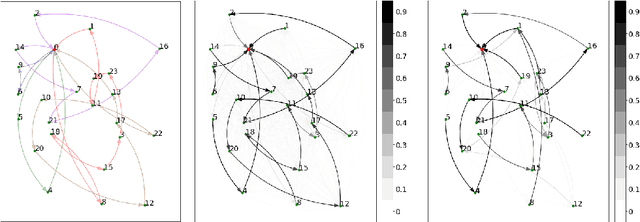
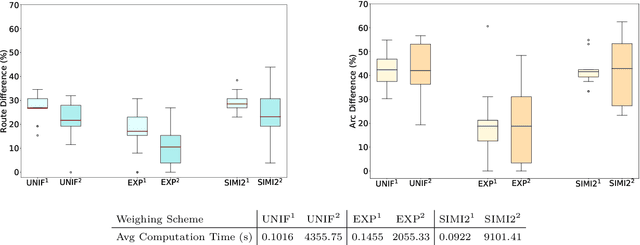
Abstract:The traditional Capacitated Vehicle Routing Problem (CVRP) minimizes the total distance of the routes under the capacity constraints of the vehicles. But more often, the objective involves multiple criteria including not only the total distance of the tour but also other factors such as travel costs, travel time, and fuel consumption.Moreover, in reality, there are numerous implicit preferences ingrained in the minds of the route planners and the drivers. Drivers, for instance, have familiarity with certain neighborhoods and knowledge of the state of roads, and often consider the best places for rest and lunch breaks. This knowledge is difficult to formulate and balance when operational routing decisions have to be made. This motivates us to learn the implicit preferences from past solutions and to incorporate these learned preferences in the optimization process. These preferences are in the form of arc probabilities, i.e., the more preferred a route is, the higher is the joint probability. The novelty of this work is the use of a neural network model to estimate the arc probabilities, which allows for additional features and automatic parameter estimation. This first requires identifying suitable features, neural architectures and loss functions, taking into account that there is typically few data available. We investigate the difference with a prior weighted Markov counting approach, and study the applicability of neural networks in this setting.
Learn-n-Route: Learning implicit preferences for vehicle routing
Jan 11, 2021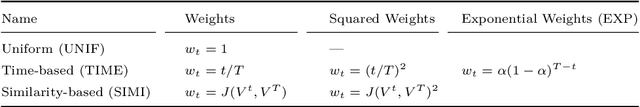

Abstract:We investigate a learning decision support system for vehicle routing, where the routing engine learns implicit preferences that human planners have when manually creating route plans (or routings). The goal is to use these learned subjective preferences on top of the distance-based objective criterion in vehicle routing systems. This is an alternative to the practice of distinctively formulating a custom VRP for every company with its own routing requirements. Instead, we assume the presence of past vehicle routing solutions over similar sets of customers, and learn to make similar choices. The learning approach is based on the concept of learning a Markov model, which corresponds to a probabilistic transition matrix, rather than a deterministic distance matrix. This nevertheless allows us to use existing arc routing VRP software in creating the actual routings, and to optimize over both distances and preferences at the same time. For the learning, we explore different schemes to construct the probabilistic transition matrix that can co-evolve with changing preferences over time. Our results on a use-case with a small transportation company show that our method is able to generate results that are close to the manually created solutions, without needing to characterize all constraints and sub-objectives explicitly. Even in the case of changes in the customer sets, our method is able to find solutions that are closer to the actual routings than when using only distances, and hence, solutions that require fewer manual changes when transformed into practical routings.
Discrete solution pools and noise-contrastive estimation for predict-and-optimize
Nov 10, 2020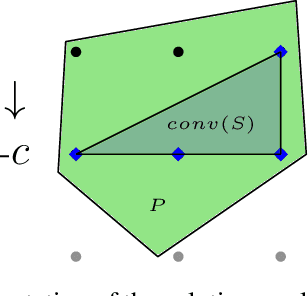


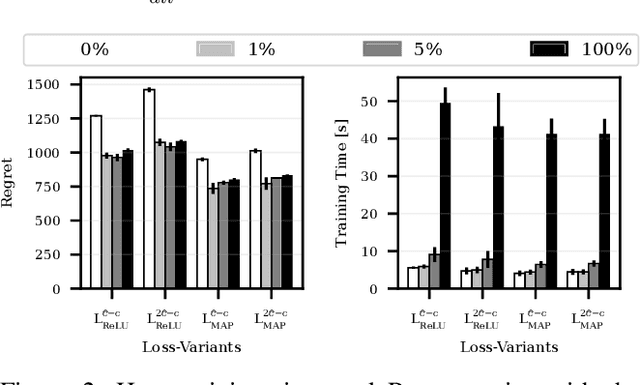
Abstract:Numerous real-life decision-making processes involve solving a combinatorial optimization problem with uncertain input that can be estimated from historic data. There is a growing interest in decision-focused learning methods, where the loss function used for learning to predict the uncertain input uses the outcome of solving the combinatorial problem over a set of predictions. Different surrogate loss functions have been identified, often using a continuous approximation of the combinatorial problem. However, a key bottleneck is that to compute the loss, one has to solve the combinatorial optimisation problem for each training instance in each epoch, which is computationally expensive even in the case of continuous approximations. We propose a different solver-agnostic method for decision-focused learning, namely by considering a pool of feasible solutions as a discrete approximation of the full combinatorial problem. Solving is now trivial through a single pass over the solution pool. We design several variants of a noise-contrastive loss over the solution pool, which we substantiate theoretically and empirically. Furthermore, we show that by dynamically re-solving only a fraction of the training instances each epoch, our method performs on par with the state of the art, whilst drastically reducing the time spent solving, hence increasing the feasibility of predict-and-optimize for larger problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge