Decision-Focused Learning: Foundations, State of the Art, Benchmark and Future Opportunities

Decision-focused learning (DFL) is an emerging paradigm in machine learning which trains a model to optimize decisions, integrating prediction and optimization in an end-to-end system. This paradigm holds the promise to revolutionize decision-making in many real-world applications which operate under uncertainty, where the estimation of unknown parameters within these decision models often becomes a substantial roadblock. This paper presents a comprehensive review of DFL. It provides an in-depth analysis of the various techniques devised to integrate machine learning and optimization models, introduces a taxonomy of DFL methods distinguished by their unique characteristics, and conducts an extensive empirical evaluation of these methods proposing suitable benchmark dataset and tasks for DFL. Finally, the study provides valuable insights into current and potential future avenues in DFL research.

Probability estimation and structured output prediction for learning preferences in last mile delivery

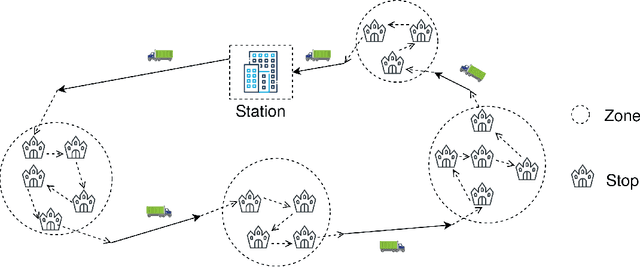
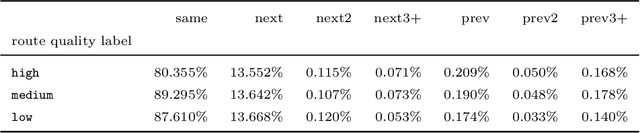
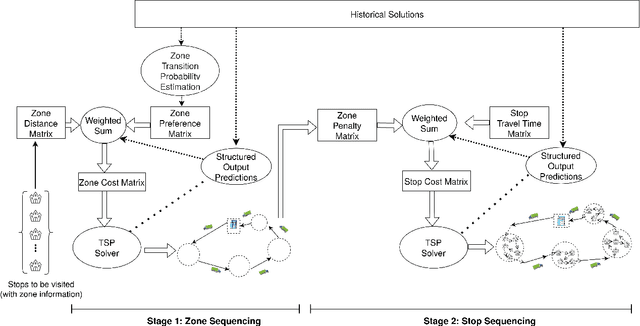
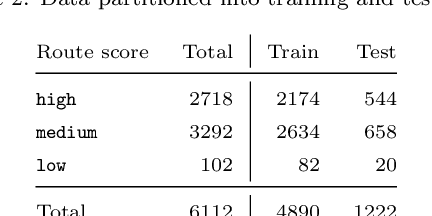
We study the problem of learning the preferences of drivers and planners in the context of last mile delivery. Given a data set containing historical decisions and delivery locations, the goal is to capture the implicit preferences of the decision-makers. We consider two ways to use the historical data: one is through a probability estimation method that learns transition probabilities between stops (or zones). This is a fast and accurate method, recently studied in a VRP setting. Furthermore, we explore the use of machine learning to infer how to best balance multiple objectives such as distance, probability and penalties. Specifically, we cast the learning problem as a structured output prediction problem, where training is done by repeatedly calling the TSP solver. Another important aspect we consider is that for last-mile delivery, every address is a potential client and hence the data is very sparse. Hence, we propose a two-stage approach that first learns preferences at the zone level in order to compute a zone routing; after which a penalty-based TSP computes the stop routing. Results show that the zone transition probability estimation performs well, and that the structured output prediction learning can improve the results further. We hence showcase a successful combination of both probability estimation and machine learning, all the while using standard TSP solvers, both during learning and to compute the final solution; this means the methodology is applicable to other, real-life, TSP variants, or proprietary solvers.

Discrete solution pools and noise-contrastive estimation for predict-and-optimize

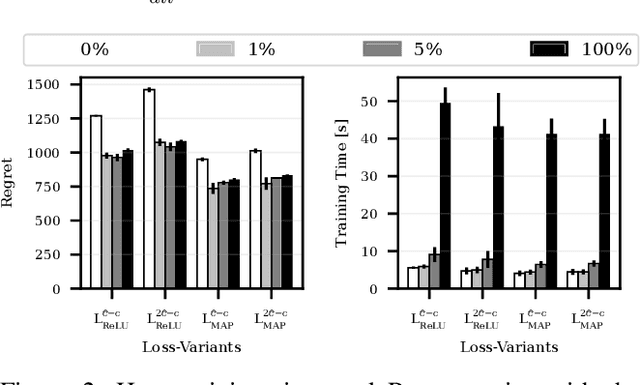
Numerous real-life decision-making processes involve solving a combinatorial optimization problem with uncertain input that can be estimated from historic data. There is a growing interest in decision-focused learning methods, where the loss function used for learning to predict the uncertain input uses the outcome of solving the combinatorial problem over a set of predictions. Different surrogate loss functions have been identified, often using a continuous approximation of the combinatorial problem. However, a key bottleneck is that to compute the loss, one has to solve the combinatorial optimisation problem for each training instance in each epoch, which is computationally expensive even in the case of continuous approximations. We propose a different solver-agnostic method for decision-focused learning, namely by considering a pool of feasible solutions as a discrete approximation of the full combinatorial problem. Solving is now trivial through a single pass over the solution pool. We design several variants of a noise-contrastive loss over the solution pool, which we substantiate theoretically and empirically. Furthermore, we show that by dynamically re-solving only a fraction of the training instances each epoch, our method performs on par with the state of the art, whilst drastically reducing the time spent solving, hence increasing the feasibility of predict-and-optimize for larger problems.