Discrete solution pools and noise-contrastive estimation for predict-and-optimize

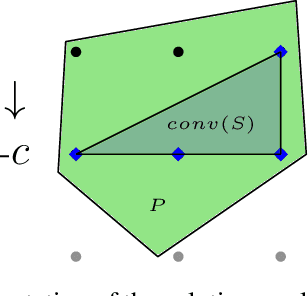
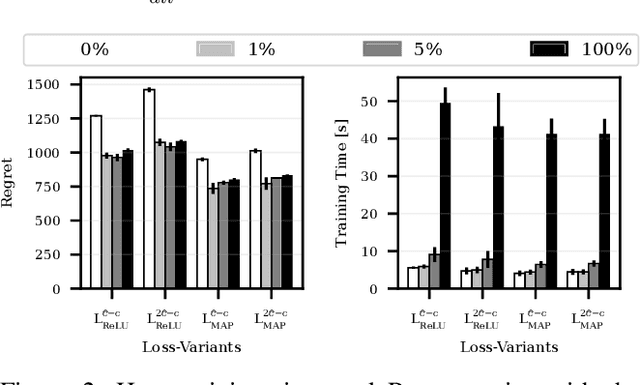
Numerous real-life decision-making processes involve solving a combinatorial optimization problem with uncertain input that can be estimated from historic data. There is a growing interest in decision-focused learning methods, where the loss function used for learning to predict the uncertain input uses the outcome of solving the combinatorial problem over a set of predictions. Different surrogate loss functions have been identified, often using a continuous approximation of the combinatorial problem. However, a key bottleneck is that to compute the loss, one has to solve the combinatorial optimisation problem for each training instance in each epoch, which is computationally expensive even in the case of continuous approximations. We propose a different solver-agnostic method for decision-focused learning, namely by considering a pool of feasible solutions as a discrete approximation of the full combinatorial problem. Solving is now trivial through a single pass over the solution pool. We design several variants of a noise-contrastive loss over the solution pool, which we substantiate theoretically and empirically. Furthermore, we show that by dynamically re-solving only a fraction of the training instances each epoch, our method performs on par with the state of the art, whilst drastically reducing the time spent solving, hence increasing the feasibility of predict-and-optimize for larger problems.