Score Function Gradient Estimation to Widen the Applicability of Decision-Focused Learning

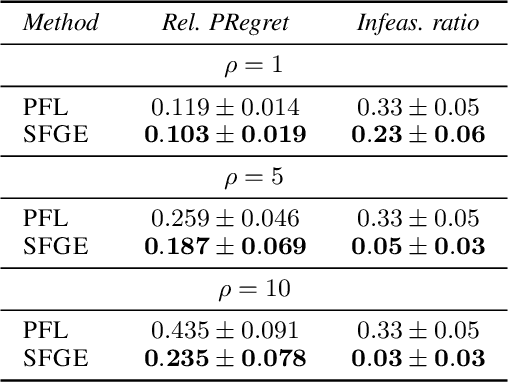
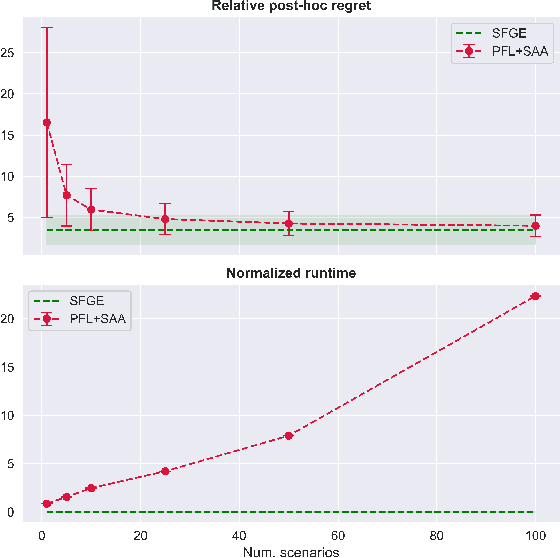
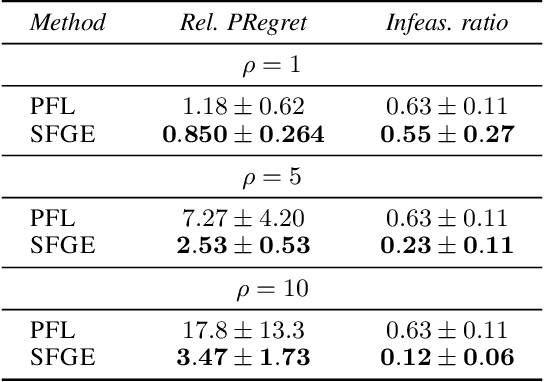
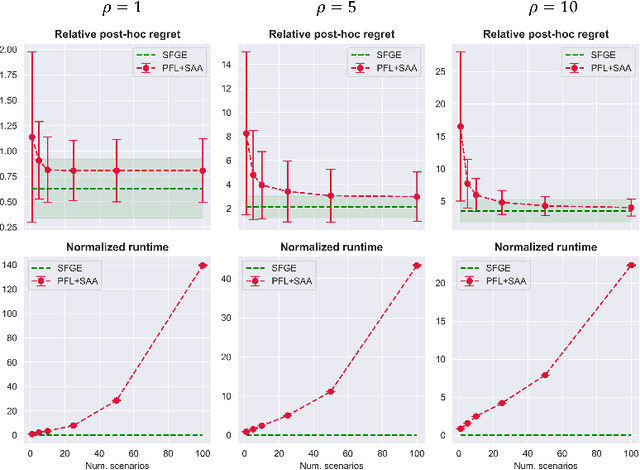
Many real-world optimization problems contain unknown parameters that must be predicted prior to solving. To train the predictive machine learning (ML) models involved, the commonly adopted approach focuses on maximizing predictive accuracy. However, this approach does not always lead to the minimization of the downstream task loss. Decision-focused learning (DFL) is a recently proposed paradigm whose goal is to train the ML model by directly minimizing the task loss. However, state-of-the-art DFL methods are limited by the assumptions they make about the structure of the optimization problem (e.g., that the problem is linear) and by the fact that can only predict parameters that appear in the objective function. In this work, we address these limitations by instead predicting \textit{distributions} over parameters and adopting score function gradient estimation (SFGE) to compute decision-focused updates to the predictive model, thereby widening the applicability of DFL. Our experiments show that by using SFGE we can: (1) deal with predictions that occur both in the objective function and in the constraints; and (2) effectively tackle two-stage stochastic optimization problems.

An analysis of Universal Differential Equations for data-driven discovery of Ordinary Differential Equations

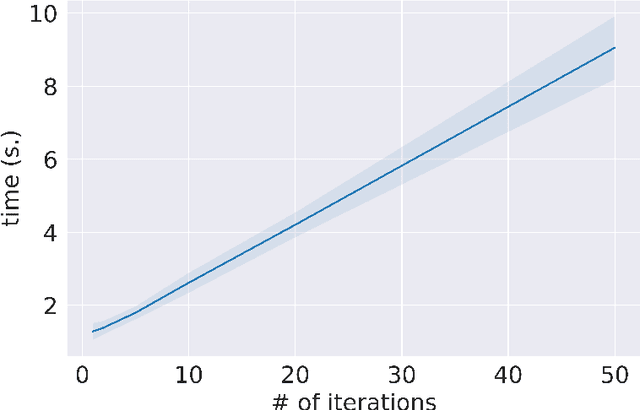
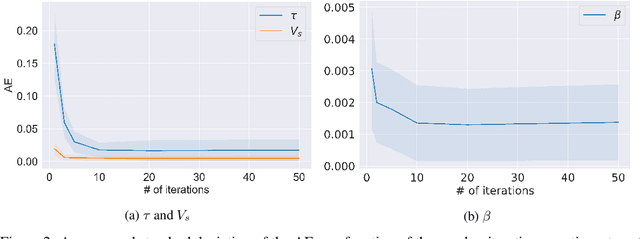
In the last decade, the scientific community has devolved its attention to the deployment of data-driven approaches in scientific research to provide accurate and reliable analysis of a plethora of phenomena. Most notably, Physics-informed Neural Networks and, more recently, Universal Differential Equations (UDEs) proved to be effective both in system integration and identification. However, there is a lack of an in-depth analysis of the proposed techniques. In this work, we make a contribution by testing the UDE framework in the context of Ordinary Differential Equations (ODEs) discovery. In our analysis, performed on two case studies, we highlight some of the issues arising when combining data-driven approaches and numerical solvers, and we investigate the importance of the data collection process. We believe that our analysis represents a significant contribution in investigating the capabilities and limitations of Physics-informed Machine Learning frameworks.

UNIFY: a Unified Policy Designing Framework for Solving Constrained Optimization Problems with Machine Learning

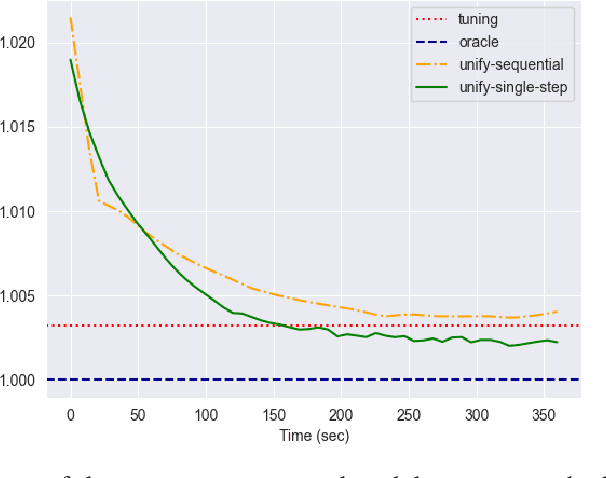
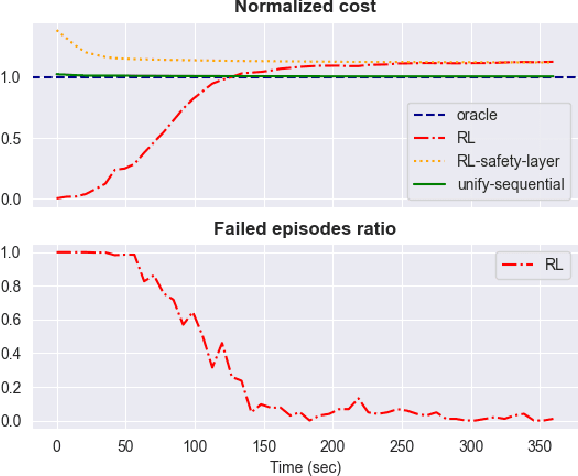
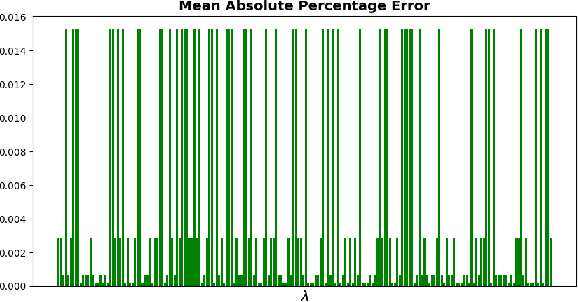
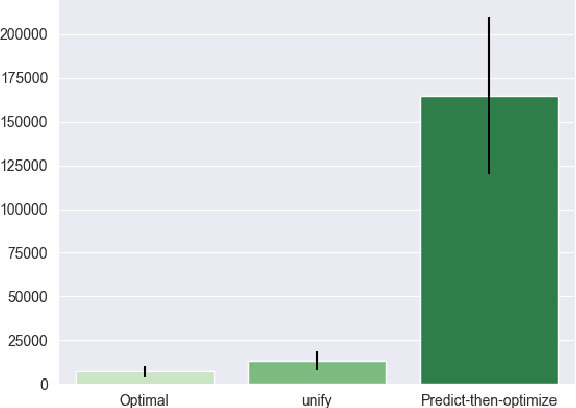
The interplay between Machine Learning (ML) and Constrained Optimization (CO) has recently been the subject of increasing interest, leading to a new and prolific research area covering (e.g.) Decision Focused Learning and Constrained Reinforcement Learning. Such approaches strive to tackle complex decision problems under uncertainty over multiple stages, involving both explicit (cost function, constraints) and implicit knowledge (from data), and possibly subject to execution time restrictions. While a good degree of success has been achieved, the existing methods still have limitations in terms of both applicability and effectiveness. For problems in this class, we propose UNIFY, a unified framework to design a solution policy for complex decision-making problems. Our approach relies on a clever decomposition of the policy in two stages, namely an unconstrained ML model and a CO problem, to take advantage of the strength of each approach while compensating for its weaknesses. With a little design effort, UNIFY can generalize several existing approaches, thus extending their applicability. We demonstrate the method effectiveness on two practical problems, namely an Energy Management System and the Set Multi-cover with stochastic coverage requirements. Finally, we highlight some current challenges of our method and future research directions that can benefit from the cross-fertilization of the two fields.

Injecting Domain Knowledge in Neural Networks: a Controlled Experiment on a Constrained Problem

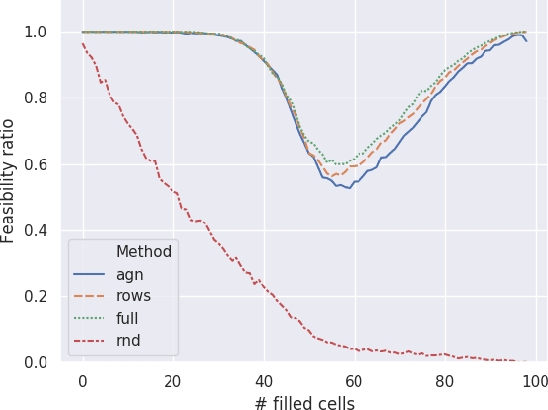
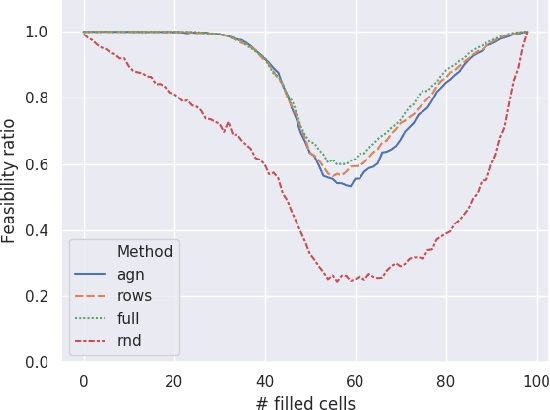
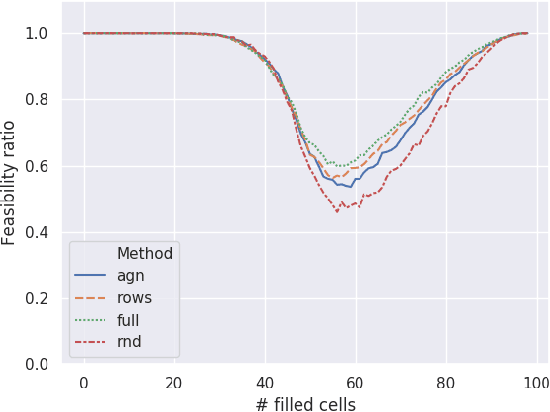
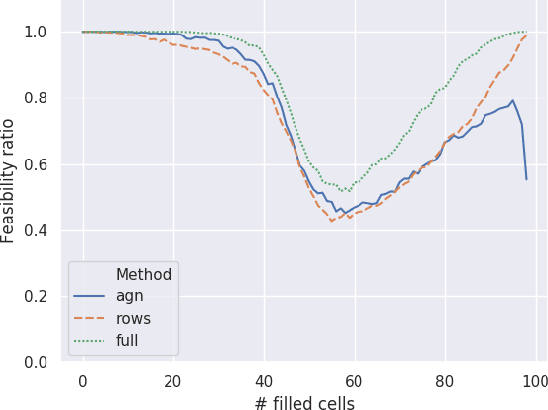
Given enough data, Deep Neural Networks (DNNs) are capable of learning complex input-output relations with high accuracy. In several domains, however, data is scarce or expensive to retrieve, while a substantial amount of expert knowledge is available. It seems reasonable that if we can inject this additional information in the DNN, we could ease the learning process. One such case is that of Constraint Problems, for which declarative approaches exists and pure ML solutions have obtained mixed success. Using a classical constrained problem as a case study, we perform controlled experiments to probe the impact of progressively adding domain and empirical knowledge in the DNN. Our results are very encouraging, showing that (at least in our setup) embedding domain knowledge at training time can have a considerable effect and that a small amount of empirical knowledge is sufficient to obtain practically useful results.