Discovering maximally consistent distribution of causal tournaments with Large Language Models

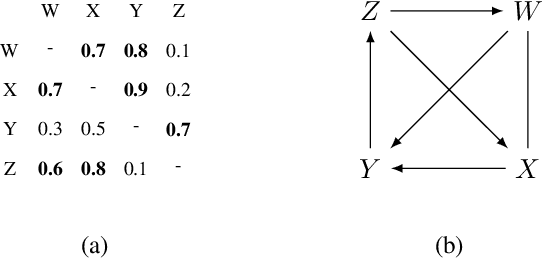
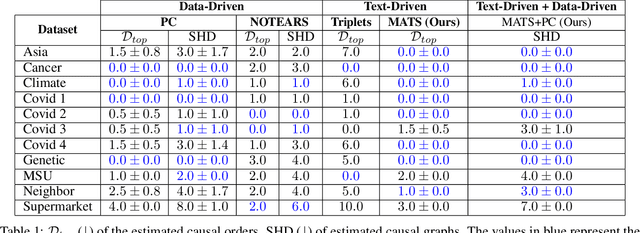
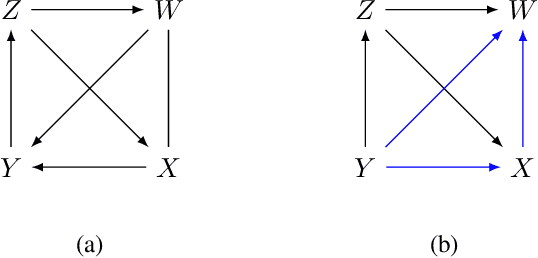
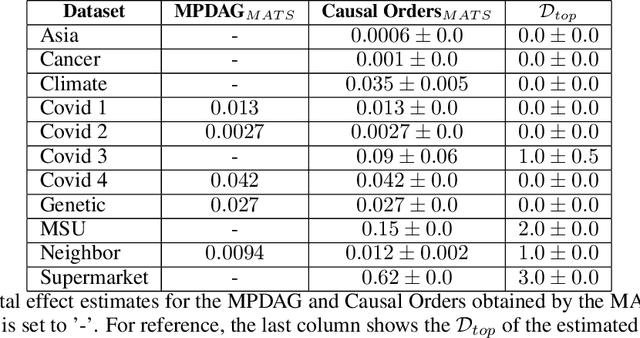
Causal discovery is essential for understanding complex systems, yet traditional methods often depend on strong, untestable assumptions, making the process challenging. Large Language Models (LLMs) present a promising alternative for extracting causal insights from text-based metadata, which consolidates domain expertise. However, LLMs are prone to unreliability and hallucinations, necessitating strategies that account for their limitations. One such strategy involves leveraging a consistency measure to evaluate reliability. Additionally, most text metadata does not clearly distinguish direct causal relationships from indirect ones, further complicating the inference of causal graphs. As a result, focusing on causal orderings, rather than causal graphs, emerges as a more practical and robust approach. We propose a novel method to derive a distribution of acyclic tournaments (representing plausible causal orders) that maximizes a consistency score. Our approach begins by computing pairwise consistency scores between variables, yielding a cyclic tournament that aggregates these scores. From this structure, we identify optimal acyclic tournaments compatible with the original tournament, prioritizing those that maximize consistency across all configurations. We tested our method on both classical and well-established bechmarks, as well as real-world datasets from epidemiology and public health. Our results demonstrate the effectiveness of our approach in recovering distributions causal orders with minimal error.

An analysis of Universal Differential Equations for data-driven discovery of Ordinary Differential Equations

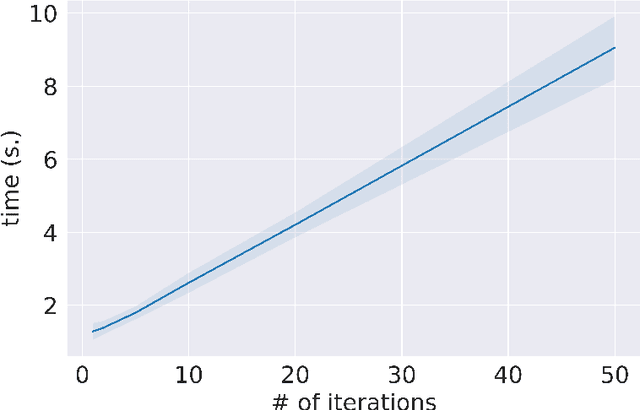
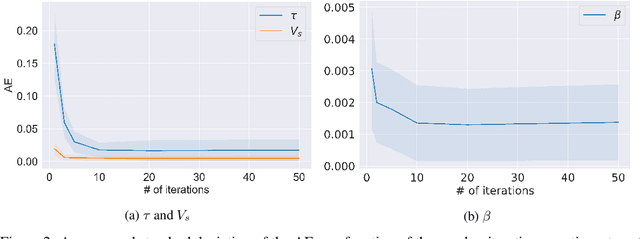
In the last decade, the scientific community has devolved its attention to the deployment of data-driven approaches in scientific research to provide accurate and reliable analysis of a plethora of phenomena. Most notably, Physics-informed Neural Networks and, more recently, Universal Differential Equations (UDEs) proved to be effective both in system integration and identification. However, there is a lack of an in-depth analysis of the proposed techniques. In this work, we make a contribution by testing the UDE framework in the context of Ordinary Differential Equations (ODEs) discovery. In our analysis, performed on two case studies, we highlight some of the issues arising when combining data-driven approaches and numerical solvers, and we investigate the importance of the data collection process. We believe that our analysis represents a significant contribution in investigating the capabilities and limitations of Physics-informed Machine Learning frameworks.

Deep Learning for Virus-Spreading Forecasting: a Brief Survey

The advent of the coronavirus pandemic has sparked the interest in predictive models capable of forecasting virus-spreading, especially for boosting and supporting decision-making processes. In this paper, we will outline the main Deep Learning approaches aimed at predicting the spreading of a disease in space and time. The aim is to show the emerging trends in this area of research and provide a general perspective on the possible strategies to approach this problem. In doing so, we will mainly focus on two macro-categories: classical Deep Learning approaches and Hybrid models. Finally, we will discuss the main advantages and disadvantages of different models, and underline the most promising development directions to improve these approaches.

An Analysis of Regularized Approaches for Constrained Machine Learning

Regularization-based approaches for injecting constraints in Machine Learning (ML) were introduced to improve a predictive model via expert knowledge. We tackle the issue of finding the right balance between the loss (the accuracy of the learner) and the regularization term (the degree of constraint satisfaction). The key results of this paper is the formal demonstration that this type of approach cannot guarantee to find all optimal solutions. In particular, in the non-convex case there might be optima for the constrained problem that do not correspond to any multiplier value.

Improving Deep Learning Models via Constraint-Based Domain Knowledge: a Brief Survey

Deep Learning (DL) models proved themselves to perform extremely well on a wide variety of learning tasks, as they can learn useful patterns from large data sets. However, purely data-driven models might struggle when very difficult functions need to be learned or when there is not enough available training data. Fortunately, in many domains prior information can be retrieved and used to boost the performance of DL models. This paper presents a first survey of the approaches devised to integrate domain knowledge, expressed in the form of constraints, in DL learning models to improve their performance, in particular targeting deep neural networks. We identify five (non-mutually exclusive) categories that encompass the main approaches to inject domain knowledge: 1) acting on the features space, 2) modifications to the hypothesis space, 3) data augmentation, 4) regularization schemes, 5) constrained learning.

Injective Domain Knowledge in Neural Networks for Transprecision Computing

Machine Learning (ML) models are very effective in many learning tasks, due to the capability to extract meaningful information from large data sets. Nevertheless, there are learning problems that cannot be easily solved relying on pure data, e.g. scarce data or very complex functions to be approximated. Fortunately, in many contexts domain knowledge is explicitly available and can be used to train better ML models. This paper studies the improvements that can be obtained by integrating prior knowledge when dealing with a non-trivial learning task, namely precision tuning of transprecision computing applications. The domain information is injected in the ML models in different ways: I) additional features, II) ad-hoc graph-based network topology, III) regularization schemes. The results clearly show that ML models exploiting problem-specific information outperform the purely data-driven ones, with an average accuracy improvement around 38%.

A Lagrangian Dual Framework for Deep Neural Networks with Constraints

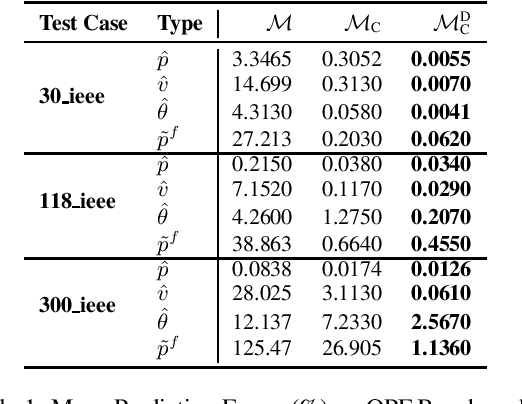
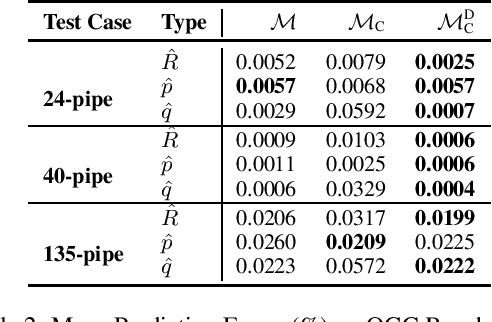
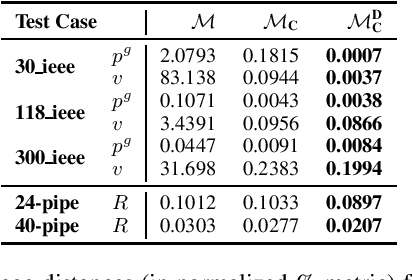
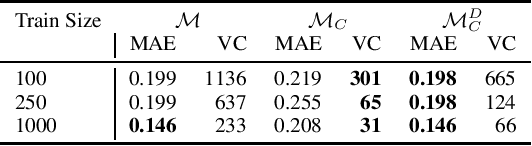
A variety of computationally challenging constrained optimization problems in several engineering disciplines are solved repeatedly under different scenarios. In many cases, they would benefit from fast and accurate approximations, either to support real-time operations or large-scale simulation studies. This paper aims at exploring how to leverage the substantial data being accumulated by repeatedly solving instances of these applications over time. It introduces a deep learning model that exploits Lagrangian duality to encourage the satisfaction of hard constraints. The proposed method is evaluated on a collection of realistic energy networks, by enforcing non-discriminatory decisions on a variety of datasets, and a transprecision computing application. The results illustrate the effectiveness of the proposed method that dramatically decreases constraint violations by the predictors and, in some applications, increases the prediction accuracy.