Bilevel Optimization for Differentially Private Optimization

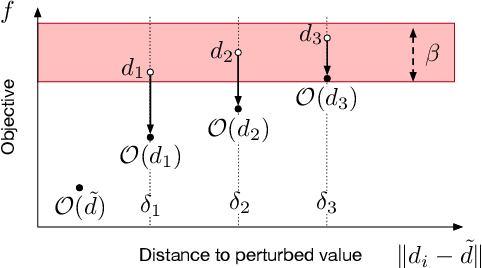
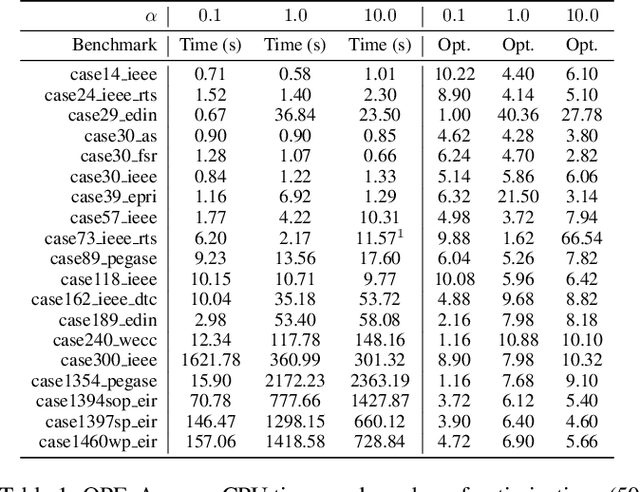
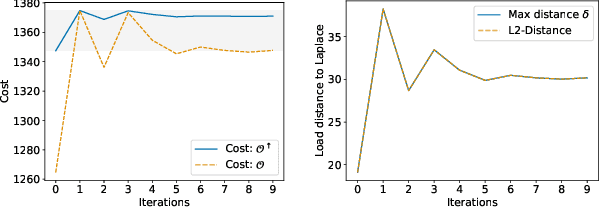
This paper studies how to apply differential privacy to constrained optimization problems whose inputs are sensitive. This task raises significant challenges since random perturbations of the input data often render the constrained optimization problem infeasible or change significantly the nature of its optimal solutions. To address this difficulty, this paper proposes a bilevel optimization model that can be used as a post-processing step: It redistributes the noise introduced by a differentially private mechanism optimally while restoring feasibility and near-optimality. The paper shows that, under a natural assumption, this bilevel model can be solved efficiently for real-life large-scale nonlinear nonconvex optimization problems with sensitive customer data. The experimental results demonstrate the accuracy of the privacy-preserving mechanism and showcase significant benefits compared to standard approaches.

A Lagrangian Dual Framework for Deep Neural Networks with Constraints

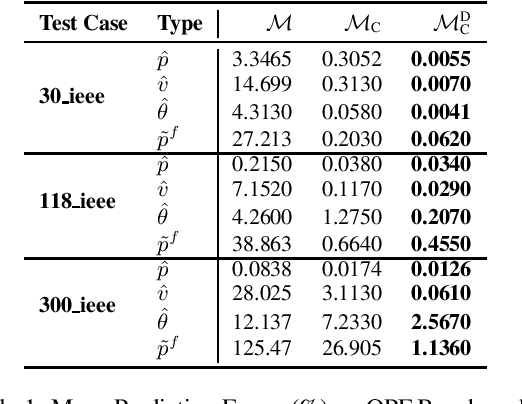
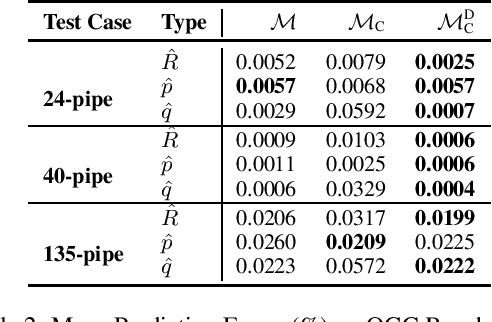
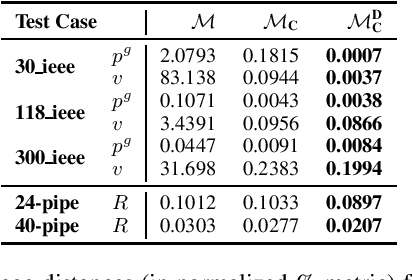
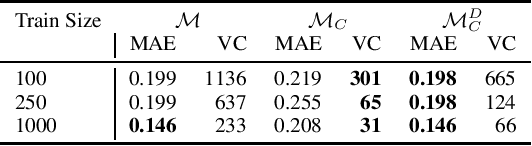
A variety of computationally challenging constrained optimization problems in several engineering disciplines are solved repeatedly under different scenarios. In many cases, they would benefit from fast and accurate approximations, either to support real-time operations or large-scale simulation studies. This paper aims at exploring how to leverage the substantial data being accumulated by repeatedly solving instances of these applications over time. It introduces a deep learning model that exploits Lagrangian duality to encourage the satisfaction of hard constraints. The proposed method is evaluated on a collection of realistic energy networks, by enforcing non-discriminatory decisions on a variety of datasets, and a transprecision computing application. The results illustrate the effectiveness of the proposed method that dramatically decreases constraint violations by the predictors and, in some applications, increases the prediction accuracy.