Simon Ferreira
Identifying Macro Causal Effects in C-DMGs
Apr 02, 2025Abstract:Causal effect identification using causal graphs is a fundamental challenge in causal inference. While extensive research has been conducted in this area, most existing methods assume the availability of fully specified causal graphs. However, in complex domains such as medicine and epidemiology, complete causal knowledge is often unavailable, and only partial information about the system is accessible. This paper focuses on causal effect identification within partially specified causal graphs, with particular emphasis on cluster-directed mixed graphs (C-DMGs). These graphs provide a higher-level representation of causal relationships by grouping variables into clusters, offering a more practical approach for handling complex systems. Unlike fully specified causal graphs, C-DMGs can contain cycles, which complicate their analysis and interpretation. Furthermore, their cluster-based nature introduces new challenges, as it gives rise to two distinct types of causal effects, macro causal effects and micro causal effects, with different properties. In this work, we focus on macro causal effects, which describe the effects of entire clusters on other clusters. We establish that the do-calculus is both sound and complete for identifying these effects in C-DMGs. Additionally, we provide a graphical characterization of non-identifiability for macro causal effects in these graphs.
Discovering maximally consistent distribution of causal tournaments with Large Language Models
Dec 18, 2024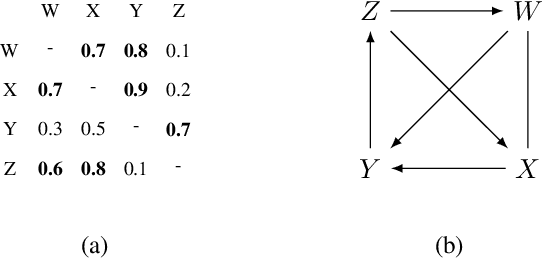
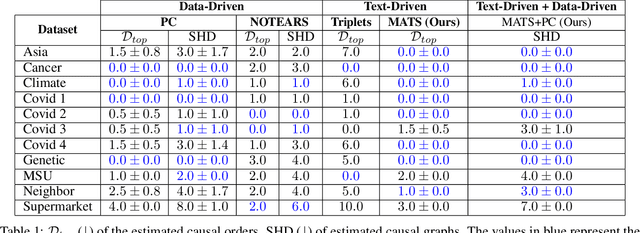
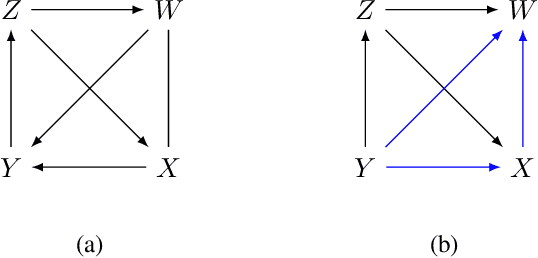
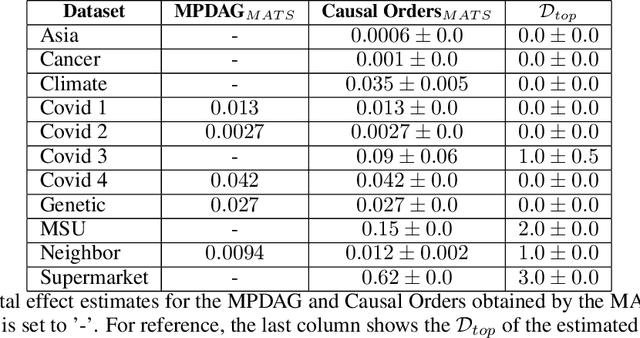
Abstract:Causal discovery is essential for understanding complex systems, yet traditional methods often depend on strong, untestable assumptions, making the process challenging. Large Language Models (LLMs) present a promising alternative for extracting causal insights from text-based metadata, which consolidates domain expertise. However, LLMs are prone to unreliability and hallucinations, necessitating strategies that account for their limitations. One such strategy involves leveraging a consistency measure to evaluate reliability. Additionally, most text metadata does not clearly distinguish direct causal relationships from indirect ones, further complicating the inference of causal graphs. As a result, focusing on causal orderings, rather than causal graphs, emerges as a more practical and robust approach. We propose a novel method to derive a distribution of acyclic tournaments (representing plausible causal orders) that maximizes a consistency score. Our approach begins by computing pairwise consistency scores between variables, yielding a cyclic tournament that aggregates these scores. From this structure, we identify optimal acyclic tournaments compatible with the original tournament, prioritizing those that maximize consistency across all configurations. We tested our method on both classical and well-established bechmarks, as well as real-world datasets from epidemiology and public health. Our results demonstrate the effectiveness of our approach in recovering distributions causal orders with minimal error.
Average Controlled and Average Natural Micro Direct Effects in Summary Causal Graphs
Oct 31, 2024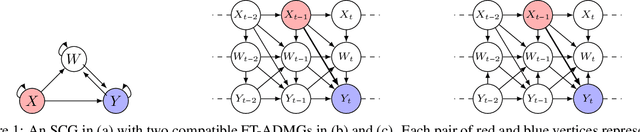
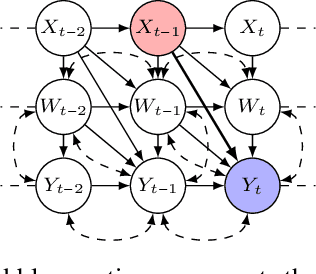
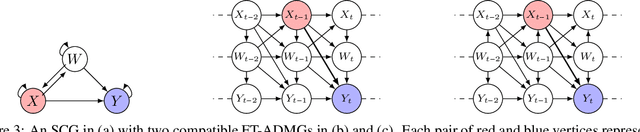
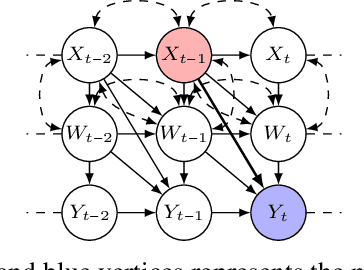
Abstract:In this paper, we investigate the identifiability of average controlled direct effects and average natural direct effects in causal systems represented by summary causal graphs, which are abstractions of full causal graphs, often used in dynamic systems where cycles and omitted temporal information complicate causal inference. Unlike in the traditional linear setting, where direct effects are typically easier to identify and estimate, non-parametric direct effects, which are crucial for handling real-world complexities, particularly in epidemiological contexts where relationships between variables (e.g, genetic, environmental, and behavioral factors) are often non-linear, are much harder to define and identify. In particular, we give sufficient conditions for identifying average controlled micro direct effect and average natural micro direct effect from summary causal graphs in the presence of hidden confounding. Furthermore, we show that the conditions given for the average controlled micro direct effect become also necessary in the setting where there is no hidden confounding and where we are only interested in identifiability by adjustment.
Identifying macro conditional independencies and macro total effects in summary causal graphs with latent confounding
Jul 10, 2024Abstract:Understanding causal relationships in dynamic systems is essential for numerous scientific fields, including epidemiology, economics, and biology. While causal inference methods have been extensively studied, they often rely on fully specified causal graphs, which may not always be available or practical in complex dynamic systems. Partially specified causal graphs, such as summary causal graphs (SCGs), provide a simplified representation of causal relationships, omitting temporal information and focusing on high-level causal structures. This simplification introduces new challenges concerning the types of queries of interest: macro queries, which involve relationships between clusters represented as vertices in the graph, and micro queries, which pertain to relationships between variables that are not directly visible through the vertices of the graph. In this paper, we first clearly distinguish between macro conditional independencies and micro conditional independencies and between macro total effects and micro total effects. Then, we demonstrate the soundness and completeness of the d-separation to identify macro conditional independencies in SCGs. Furthermore, we establish that the do-calculus is sound and complete for identifying macro total effects in SCGs. Conversely, we also show through various examples that these results do not hold when considering micro conditional independencies and micro total effects.
Case Studies of Causal Discovery from IT Monitoring Time Series
Jul 28, 2023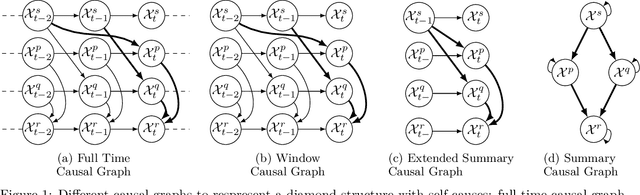
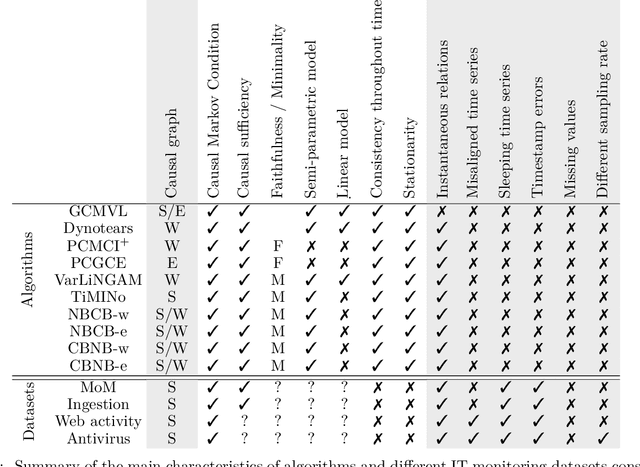
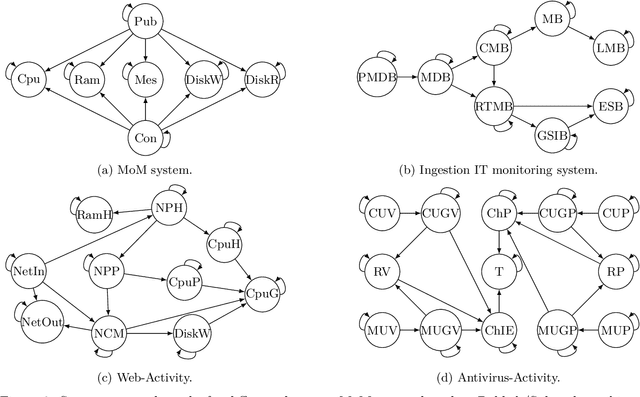
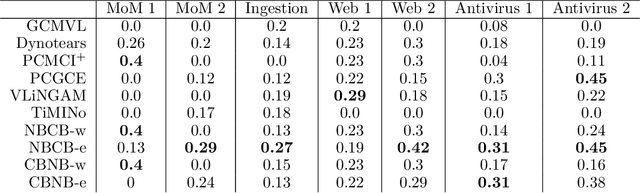
Abstract:Information technology (IT) systems are vital for modern businesses, handling data storage, communication, and process automation. Monitoring these systems is crucial for their proper functioning and efficiency, as it allows collecting extensive observational time series data for analysis. The interest in causal discovery is growing in IT monitoring systems as knowing causal relations between different components of the IT system helps in reducing downtime, enhancing system performance and identifying root causes of anomalies and incidents. It also allows proactive prediction of future issues through historical data analysis. Despite its potential benefits, applying causal discovery algorithms on IT monitoring data poses challenges, due to the complexity of the data. For instance, IT monitoring data often contains misaligned time series, sleeping time series, timestamp errors and missing values. This paper presents case studies on applying causal discovery algorithms to different IT monitoring datasets, highlighting benefits and ongoing challenges.
Identifiability of direct effects from summary causal graphs
Jun 29, 2023Abstract:Dynamic structural causal models (SCMs) are a powerful framework for reasoning in dynamic systems about direct effects which measure how a change in one variable affects another variable while holding all other variables constant. The causal relations in a dynamic structural causal model can be qualitatively represented with a full-time causal graph. Assuming linearity and causal sufficiency and given the full-time causal graph, the direct causal effect is always identifiable and can be estimated from data by adjusting on any set of variables given by the so-called single-door criterion. However, in many application such a graph is not available for various reasons but nevertheless experts have access to an abstraction of the full-time causal graph which represents causal relations between time series while omitting temporal information. This paper presents a complete identifiability result which characterizes all cases for which the direct effect is graphically identifiable from summary causal graphs and gives two sound finite adjustment sets that can be used to estimate the direct effect whenever it is identifiable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge