Score Function Gradient Estimation to Widen the Applicability of Decision-Focused Learning

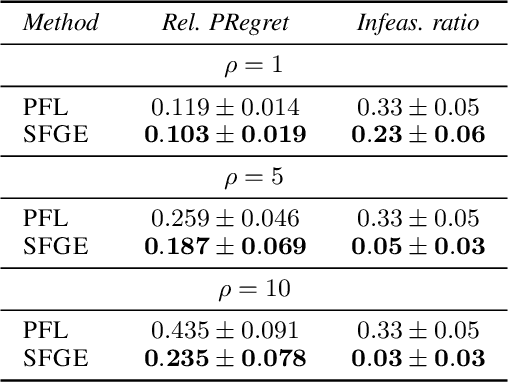
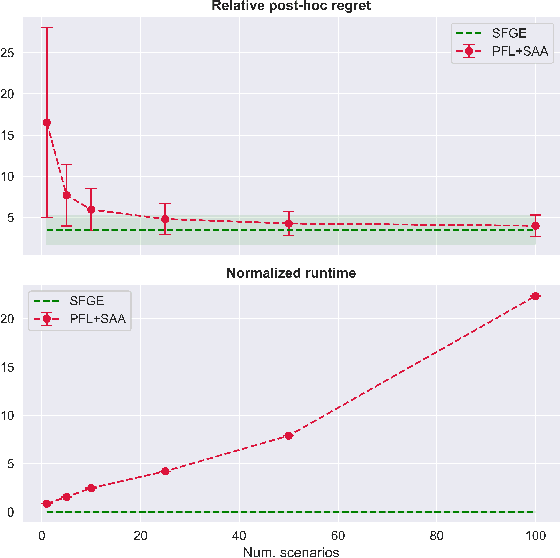
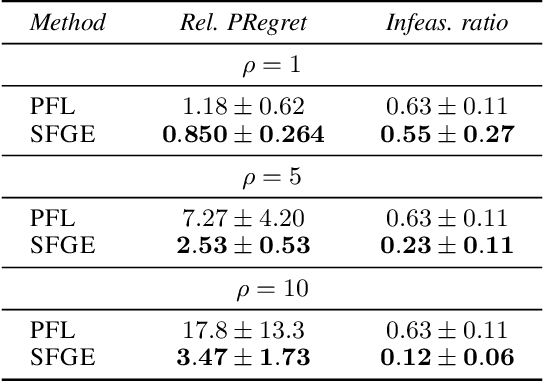
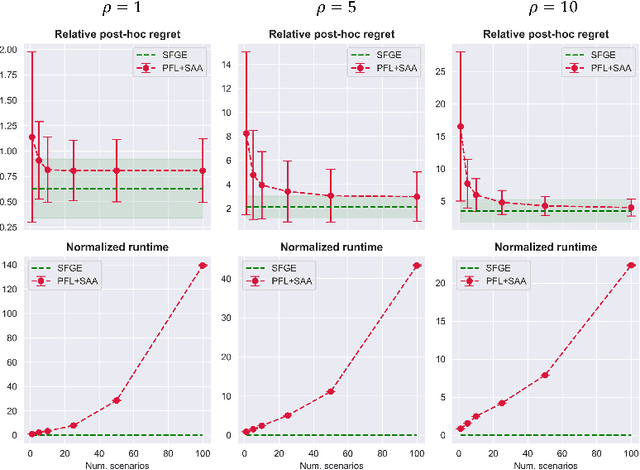
Many real-world optimization problems contain unknown parameters that must be predicted prior to solving. To train the predictive machine learning (ML) models involved, the commonly adopted approach focuses on maximizing predictive accuracy. However, this approach does not always lead to the minimization of the downstream task loss. Decision-focused learning (DFL) is a recently proposed paradigm whose goal is to train the ML model by directly minimizing the task loss. However, state-of-the-art DFL methods are limited by the assumptions they make about the structure of the optimization problem (e.g., that the problem is linear) and by the fact that can only predict parameters that appear in the objective function. In this work, we address these limitations by instead predicting \textit{distributions} over parameters and adopting score function gradient estimation (SFGE) to compute decision-focused updates to the predictive model, thereby widening the applicability of DFL. Our experiments show that by using SFGE we can: (1) deal with predictions that occur both in the objective function and in the constraints; and (2) effectively tackle two-stage stochastic optimization problems.

UNIFY: a Unified Policy Designing Framework for Solving Constrained Optimization Problems with Machine Learning

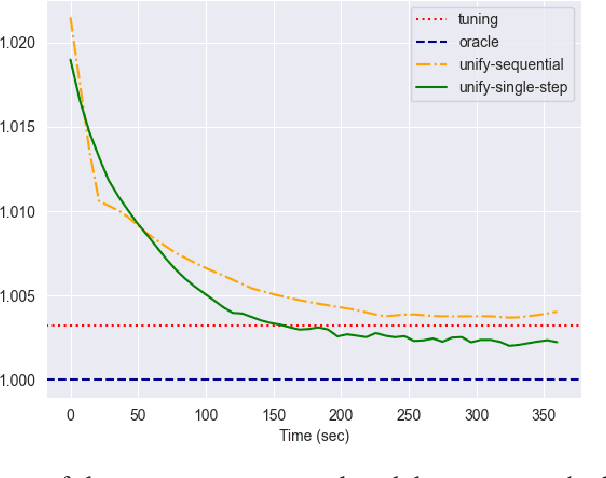
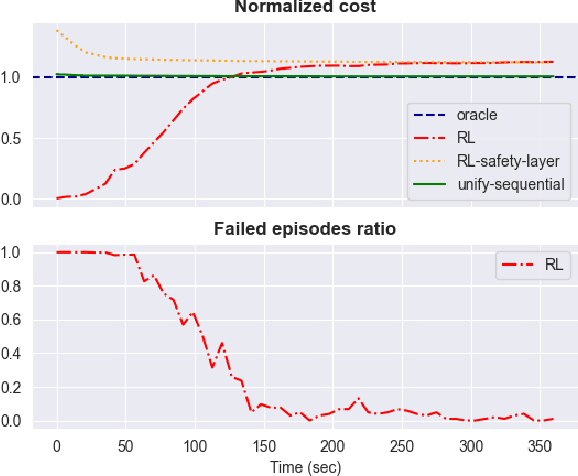
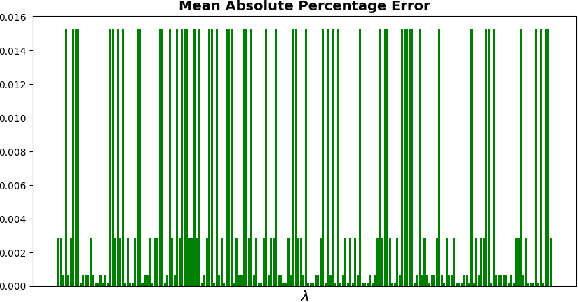
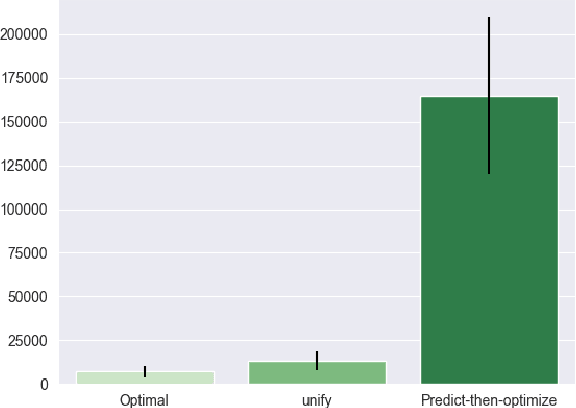
The interplay between Machine Learning (ML) and Constrained Optimization (CO) has recently been the subject of increasing interest, leading to a new and prolific research area covering (e.g.) Decision Focused Learning and Constrained Reinforcement Learning. Such approaches strive to tackle complex decision problems under uncertainty over multiple stages, involving both explicit (cost function, constraints) and implicit knowledge (from data), and possibly subject to execution time restrictions. While a good degree of success has been achieved, the existing methods still have limitations in terms of both applicability and effectiveness. For problems in this class, we propose UNIFY, a unified framework to design a solution policy for complex decision-making problems. Our approach relies on a clever decomposition of the policy in two stages, namely an unconstrained ML model and a CO problem, to take advantage of the strength of each approach while compensating for its weaknesses. With a little design effort, UNIFY can generalize several existing approaches, thus extending their applicability. We demonstrate the method effectiveness on two practical problems, namely an Energy Management System and the Set Multi-cover with stochastic coverage requirements. Finally, we highlight some current challenges of our method and future research directions that can benefit from the cross-fertilization of the two fields.