Decision-focused predictions via pessimistic bilevel optimization: a computational study

Dealing with uncertainty in optimization parameters is an important and longstanding challenge. Typically, uncertain parameters are predicted accurately, and then a deterministic optimization problem is solved. However, the decisions produced by this so-called \emph{predict-then-optimize} procedure can be highly sensitive to uncertain parameters. In this work, we contribute to recent efforts in producing \emph{decision-focused} predictions, i.e., to build predictive models that are constructed with the goal of minimizing a \emph{regret} measure on the decisions taken with them. We formulate the exact expected regret minimization as a pessimistic bilevel optimization model. Then, using duality arguments, we reformulate it as a non-convex quadratic optimization problem. Finally, we show various computational techniques to achieve tractability. We report extensive computational results on shortest-path instances with uncertain cost vectors. Our results indicate that our approach can improve training performance over the approach of Elmachtoub and Grigas (2022), a state-of-the-art method for decision-focused learning.

Predict and Optimize: Through the Lens of Learning to Rank

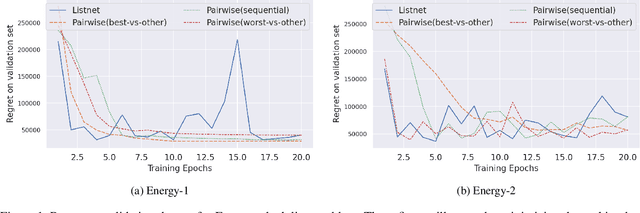
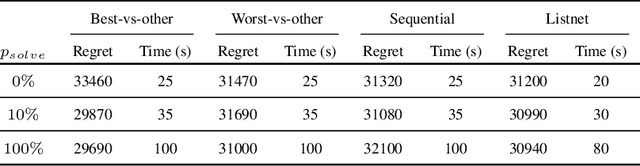
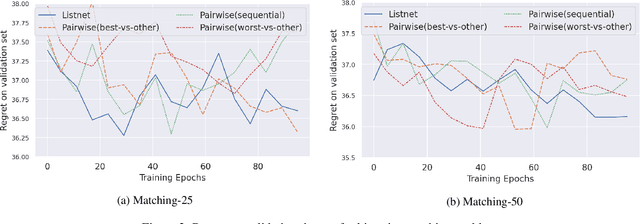
In the last years predict-and-optimize approaches (Elmachtoub and Grigas 2021; Wilder, Dilkina, and Tambe 2019) have received increasing attention. These problems have the settings where the predictions of predictive machine learning (ML) models are fed to downstream optimization problems for decision making. Predict-and-optimize approaches propose to train the ML models, often neural network models, by directly optimizing the quality of decisions made by the optimization solvers. However, one major bottleneck of predict-and-optimize approaches is solving the optimization problem for each training instance at every epoch. To address this challenge, Mulamba et al. (2021) propose noise contrastive estimation by caching feasible solutions. In this work, we show the noise contrastive estimation can be considered a case of learning to rank the solution cache. We also develop pairwise and listwise ranking loss functions, which can be differentiated in closed form without the need of solving the optimization problem. By training with respect to these surrogate loss function, we empirically show that we are able to minimize the regret of the predictions.

Data Driven VRP: A Neural Network Model to Learn Hidden Preferences for VRP

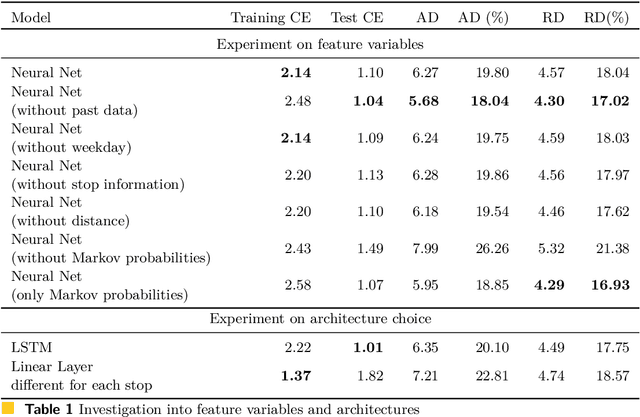
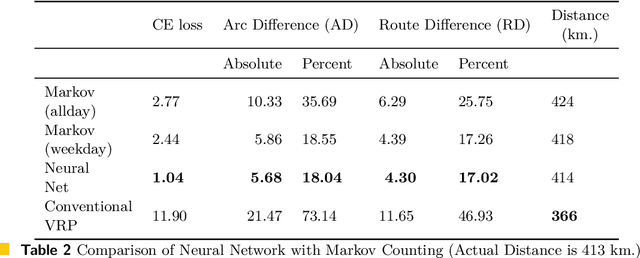
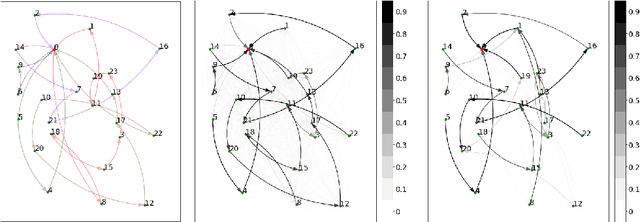
The traditional Capacitated Vehicle Routing Problem (CVRP) minimizes the total distance of the routes under the capacity constraints of the vehicles. But more often, the objective involves multiple criteria including not only the total distance of the tour but also other factors such as travel costs, travel time, and fuel consumption.Moreover, in reality, there are numerous implicit preferences ingrained in the minds of the route planners and the drivers. Drivers, for instance, have familiarity with certain neighborhoods and knowledge of the state of roads, and often consider the best places for rest and lunch breaks. This knowledge is difficult to formulate and balance when operational routing decisions have to be made. This motivates us to learn the implicit preferences from past solutions and to incorporate these learned preferences in the optimization process. These preferences are in the form of arc probabilities, i.e., the more preferred a route is, the higher is the joint probability. The novelty of this work is the use of a neural network model to estimate the arc probabilities, which allows for additional features and automatic parameter estimation. This first requires identifying suitable features, neural architectures and loss functions, taking into account that there is typically few data available. We investigate the difference with a prior weighted Markov counting approach, and study the applicability of neural networks in this setting.

Learn-n-Route: Learning implicit preferences for vehicle routing

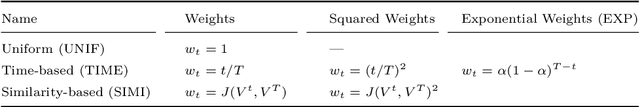
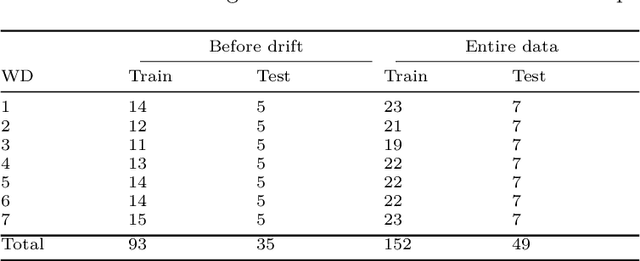
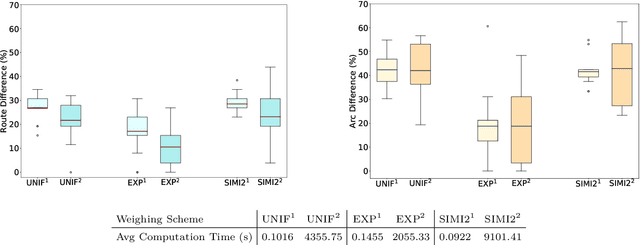
We investigate a learning decision support system for vehicle routing, where the routing engine learns implicit preferences that human planners have when manually creating route plans (or routings). The goal is to use these learned subjective preferences on top of the distance-based objective criterion in vehicle routing systems. This is an alternative to the practice of distinctively formulating a custom VRP for every company with its own routing requirements. Instead, we assume the presence of past vehicle routing solutions over similar sets of customers, and learn to make similar choices. The learning approach is based on the concept of learning a Markov model, which corresponds to a probabilistic transition matrix, rather than a deterministic distance matrix. This nevertheless allows us to use existing arc routing VRP software in creating the actual routings, and to optimize over both distances and preferences at the same time. For the learning, we explore different schemes to construct the probabilistic transition matrix that can co-evolve with changing preferences over time. Our results on a use-case with a small transportation company show that our method is able to generate results that are close to the manually created solutions, without needing to characterize all constraints and sub-objectives explicitly. Even in the case of changes in the customer sets, our method is able to find solutions that are closer to the actual routings than when using only distances, and hence, solutions that require fewer manual changes when transformed into practical routings.