Tightening convex relaxations of trained neural networks: a unified approach for convex and S-shaped activations

The non-convex nature of trained neural networks has created significant obstacles in their incorporation into optimization models. Considering the wide array of applications that this embedding has, the optimization and deep learning communities have dedicated significant efforts to the convexification of trained neural networks. Many approaches to date have considered obtaining convex relaxations for each non-linear activation in isolation, which poses limitations in the tightness of the relaxations. Anderson et al. (2020) strengthened these relaxations and provided a framework to obtain the convex hull of the graph of a piecewise linear convex activation composed with an affine function; this effectively convexifies activations such as the ReLU together with the affine transformation that precedes it. In this article, we contribute to this line of work by developing a recursive formula that yields a tight convexification for the composition of an activation with an affine function for a wide scope of activation functions, namely, convex or ``S-shaped". Our approach can be used to efficiently compute separating hyperplanes or determine that none exists in various settings, including non-polyhedral cases. We provide computational experiments to test the empirical benefits of these convex approximations.

Decision-focused predictions via pessimistic bilevel optimization: a computational study

Dealing with uncertainty in optimization parameters is an important and longstanding challenge. Typically, uncertain parameters are predicted accurately, and then a deterministic optimization problem is solved. However, the decisions produced by this so-called \emph{predict-then-optimize} procedure can be highly sensitive to uncertain parameters. In this work, we contribute to recent efforts in producing \emph{decision-focused} predictions, i.e., to build predictive models that are constructed with the goal of minimizing a \emph{regret} measure on the decisions taken with them. We formulate the exact expected regret minimization as a pessimistic bilevel optimization model. Then, using duality arguments, we reformulate it as a non-convex quadratic optimization problem. Finally, we show various computational techniques to achieve tractability. We report extensive computational results on shortest-path instances with uncertain cost vectors. Our results indicate that our approach can improve training performance over the approach of Elmachtoub and Grigas (2022), a state-of-the-art method for decision-focused learning.

Computational Tradeoffs of Optimization-Based Bound Tightening in ReLU Networks

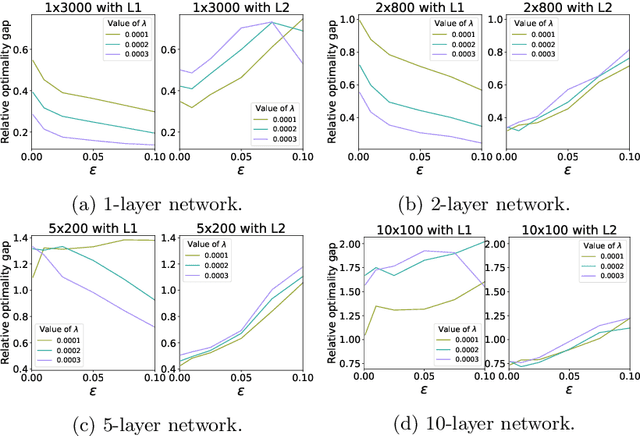
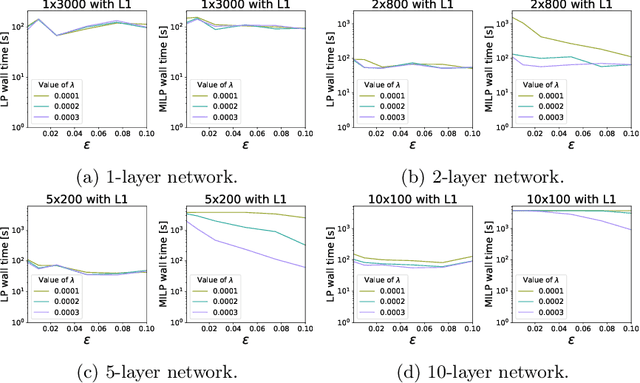
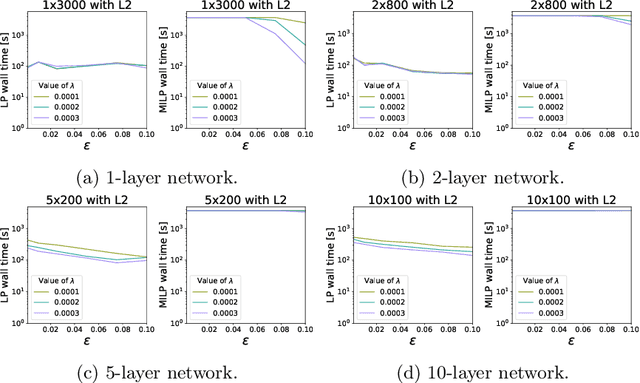
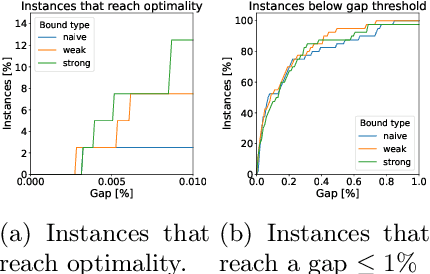
The use of Mixed-Integer Linear Programming (MILP) models to represent neural networks with Rectified Linear Unit (ReLU) activations has become increasingly widespread in the last decade. This has enabled the use of MILP technology to test-or stress-their behavior, to adversarially improve their training, and to embed them in optimization models leveraging their predictive power. Many of these MILP models rely on activation bounds. That is, bounds on the input values of each neuron. In this work, we explore the tradeoff between the tightness of these bounds and the computational effort of solving the resulting MILP models. We provide guidelines for implementing these models based on the impact of network structure, regularization, and rounding.

When Deep Learning Meets Polyhedral Theory: A Survey

In the past decade, deep learning became the prevalent methodology for predictive modeling thanks to the remarkable accuracy of deep neural networks in tasks such as computer vision and natural language processing. Meanwhile, the structure of neural networks converged back to simpler representations based on piecewise constant and piecewise linear functions such as the Rectified Linear Unit (ReLU), which became the most commonly used type of activation function in neural networks. That made certain types of network structure $\unicode{x2014}$such as the typical fully-connected feedforward neural network$\unicode{x2014}$ amenable to analysis through polyhedral theory and to the application of methodologies such as Linear Programming (LP) and Mixed-Integer Linear Programming (MILP) for a variety of purposes. In this paper, we survey the main topics emerging from this fast-paced area of work, which bring a fresh perspective to understanding neural networks in more detail as well as to applying linear optimization techniques to train, verify, and reduce the size of such networks.

Principled Deep Neural Network Training through Linear Programming

Deep Learning has received significant attention due to its impressive performance in many state-of-the-art learning tasks. Unfortunately, while very powerful, Deep Learning is not well understood theoretically and in particular only recently results for the complexity of training deep neural networks have been obtained. In this work we show that large classes of deep neural networks with various architectures (e.g., DNNs, CNNs, Binary Neural Networks, and ResNets), activation functions (e.g., ReLUs and leaky ReLUs), and loss functions (e.g., Hinge loss, Euclidean loss, etc) can be trained to near optimality with desired target accuracy using linear programming in time that is exponential in the size of the architecture and polynomial in the size of the data set; this is the best one can hope for due to the NP-Hardness of the problem and in line with previous work. In particular, we obtain polynomial time algorithms for training for a given fixed network architecture. Our work applies more broadly to empirical risk minimization problems which allows us to generalize various previous results and obtain new complexity results for previously unstudied architectures in the proper learning setting.