Computational Tradeoffs of Optimization-Based Bound Tightening in ReLU Networks
Paper and Code
Dec 27, 2023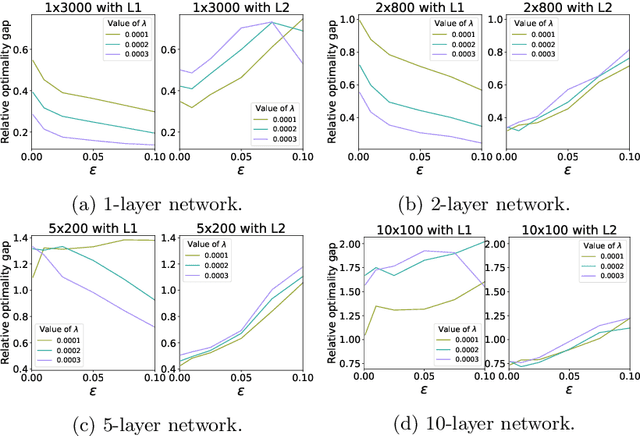
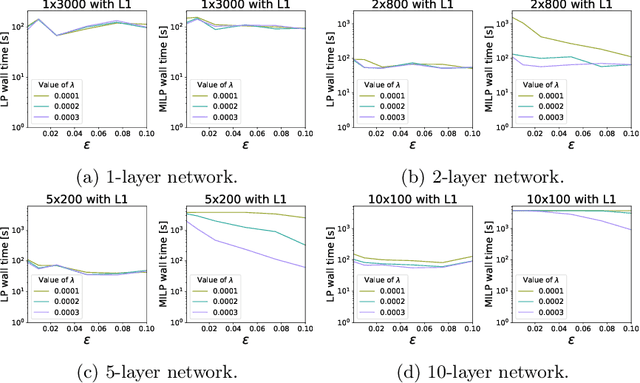
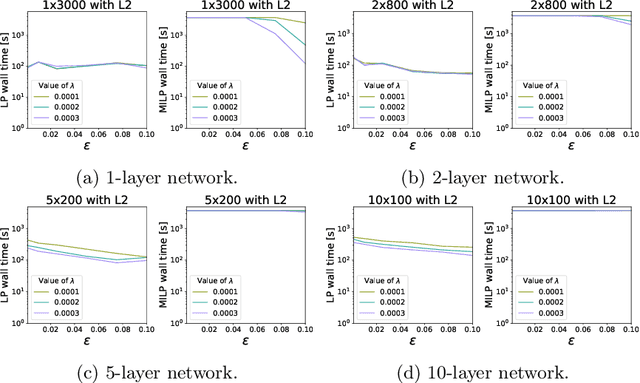
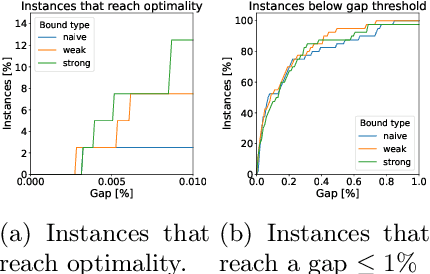
The use of Mixed-Integer Linear Programming (MILP) models to represent neural networks with Rectified Linear Unit (ReLU) activations has become increasingly widespread in the last decade. This has enabled the use of MILP technology to test-or stress-their behavior, to adversarially improve their training, and to embed them in optimization models leveraging their predictive power. Many of these MILP models rely on activation bounds. That is, bounds on the input values of each neuron. In this work, we explore the tradeoff between the tightness of these bounds and the computational effort of solving the resulting MILP models. We provide guidelines for implementing these models based on the impact of network structure, regularization, and rounding.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge