Evaluation and Verification of Physics-Informed Neural Models of the Grad-Shafranov Equation

Our contributions are motivated by fusion reactors that rely on maintaining magnetohydrodynamic (MHD) equilibrium, where the balance between plasma pressure and confining magnetic fields is required for stable operation. In axisymmetric tokamak reactors in particular, and under the assumption of toroidal symmetry, this equilibrium can be mathematically modelled using the Grad-Shafranov Equation (GSE). Recent works have demonstrated the potential of using Physics-Informed Neural Networks (PINNs) to model the GSE. Existing studies did not examine realistic scenarios in which a single network generalizes to a variety of boundary conditions. Addressing that limitation, we evaluate a PINN architecture that incorporates boundary points as network inputs. Additionally, we compare PINN model accuracy and inference speeds with a Fourier Neural Operator (FNO) model. Finding the PINN model to be the most performant, and accurate in our setting, we use the network verification tool Marabou to perform a range of verification tasks. Although we find some discrepancies between evaluations of the networks natively in PyTorch, compared to via Marabou, we are able to demonstrate useful and practical verification workflows. Our study is the first investigation of verification of such networks.

Fried Parameter Estimation from Single Wavefront Sensor Image with Artificial Neural Networks

Atmospheric turbulence degrades the quality of astronomical observations in ground-based telescopes, leading to distorted and blurry images. Adaptive Optics (AO) systems are designed to counteract these effects, using atmospheric measurements captured by a wavefront sensor to make real-time corrections to the incoming wavefront. The Fried parameter, r0, characterises the strength of atmospheric turbulence and is an essential control parameter for optimising the performance of AO systems and more recently sky profiling for Free Space Optical (FSO) communication channels. In this paper, we develop a novel data-driven approach, adapting machine learning methods from computer vision for Fried parameter estimation from a single Shack-Hartmann or pyramid wavefront sensor image. Using these data-driven methods, we present a detailed simulation-based evaluation of our approach using the open-source COMPASS AO simulation tool to evaluate both the Shack-Hartmann and pyramid wavefront sensors. Our evaluation is over a range of guide star magnitudes, and realistic noise, atmospheric and instrument conditions. Remarkably, we are able to develop a single network-based estimator that is accurate in both open and closed-loop AO configurations. Our method accurately estimates the Fried parameter from a single WFS image directly from AO telemetry to a few millimetres. Our approach is suitable for real time control, exhibiting 0.83ms r0 inference times on retail NVIDIA RTX 3090 GPU hardware, and thereby demonstrating a compelling economic solution for use in real-time instrument control.

Computer Assisted Composition in Continuous Time

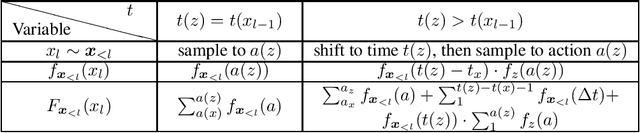
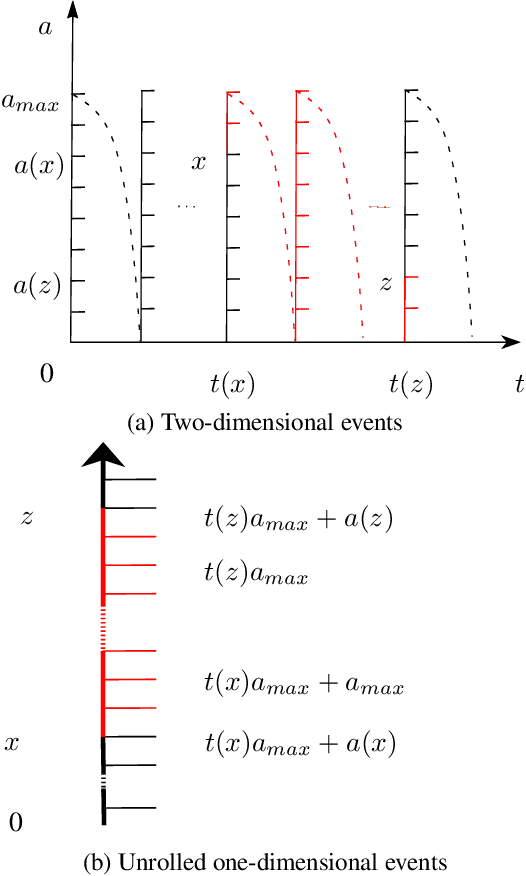
We address the problem of combining sequence models of symbolic music with user defined constraints. For typical models this is non-trivial as only the conditional distribution of each symbol given the earlier symbols is available, while the constraints correspond to arbitrary times. Previously this has been addressed by assuming a discrete time model of fixed rhythm. We generalise to continuous time and arbitrary rhythm by introducing a simple, novel, and efficient particle filter scheme, applicable to general continuous time point processes. Extensive experimental evaluations demonstrate that in comparison with a more traditional beam search baseline, the particle filter exhibits superior statistical properties and yields more agreeable results in an extensive human listening test experiment.

A Study of Proxies for Shapley Allocations of Transport Costs

We propose and evaluate a number of solutions to the problem of calculating the cost to serve each location in a single-vehicle transport setting. Such cost to serve analysis has application both strategically and operationally in transportation. The problem is formally given by the traveling salesperson game (TSG), a cooperative total utility game in which agents correspond to locations in a traveling salesperson problem (TSP). The cost to serve a location is an allocated portion of the cost of an optimal tour. The Shapley value is one of the most important normative division schemes in cooperative games, giving a principled and fair allocation both for the TSG and more generally. We consider a number of direct and sampling-based procedures for calculating the Shapley value, and present the first proof that approximating the Shapley value of the TSG within a constant factor is NP-hard. Treating the Shapley value as an ideal baseline allocation, we then develop six proxies for that value which are relatively easy to compute. We perform an experimental evaluation using Synthetic Euclidean games as well as games derived from real-world tours calculated for fast-moving consumer goods scenarios. Our experiments show that several computationally tractable allocation techniques correspond to good proxies for the Shapley value.

Implementation and Comparison of Solution Methods for Decision Processes with Non-Markovian Rewards

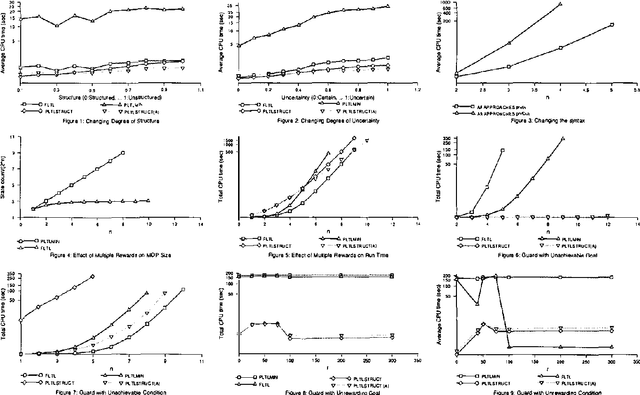
This paper examines a number of solution methods for decision processes with non-Markovian rewards (NMRDPs). They all exploit a temporal logic specification of the reward function to automatically translate the NMRDP into an equivalent Markov decision process (MDP) amenable to well-known MDP solution methods. They differ however in the representation of the target MDP and the class of MDP solution methods to which they are suited. As a result, they adopt different temporal logics and different translations. Unfortunately, no implementation of these methods nor experimental let alone comparative results have ever been reported. This paper is the first step towards filling this gap. We describe an integrated system for solving NMRDPs which implements these methods and several variants under a common interface; we use it to compare the various approaches and identify the problem features favoring one over the other.

Exploiting First-Order Regression in Inductive Policy Selection

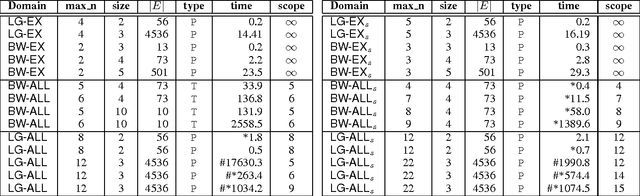
We consider the problem of computing optimal generalised policies for relational Markov decision processes. We describe an approach combining some of the benefits of purely inductive techniques with those of symbolic dynamic programming methods. The latter reason about the optimal value function using first-order decision theoretic regression and formula rewriting, while the former, when provided with a suitable hypotheses language, are capable of generalising value functions or policies for small instances. Our idea is to use reasoning and in particular classical first-order regression to automatically generate a hypotheses language dedicated to the domain at hand, which is then used as input by an inductive solver. This approach avoids the more complex reasoning of symbolic dynamic programming while focusing the inductive solver's attention on concepts that are specifically relevant to the optimal value function for the domain considered.