Exploiting First-Order Regression in Inductive Policy Selection

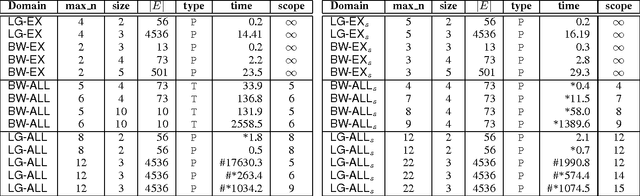
We consider the problem of computing optimal generalised policies for relational Markov decision processes. We describe an approach combining some of the benefits of purely inductive techniques with those of symbolic dynamic programming methods. The latter reason about the optimal value function using first-order decision theoretic regression and formula rewriting, while the former, when provided with a suitable hypotheses language, are capable of generalising value functions or policies for small instances. Our idea is to use reasoning and in particular classical first-order regression to automatically generate a hypotheses language dedicated to the domain at hand, which is then used as input by an inductive solver. This approach avoids the more complex reasoning of symbolic dynamic programming while focusing the inductive solver's attention on concepts that are specifically relevant to the optimal value function for the domain considered.