Encoding Linear Constraints into SAT

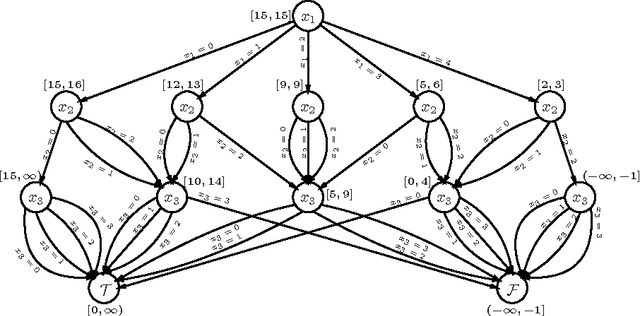
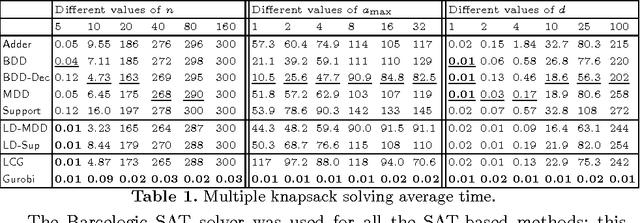
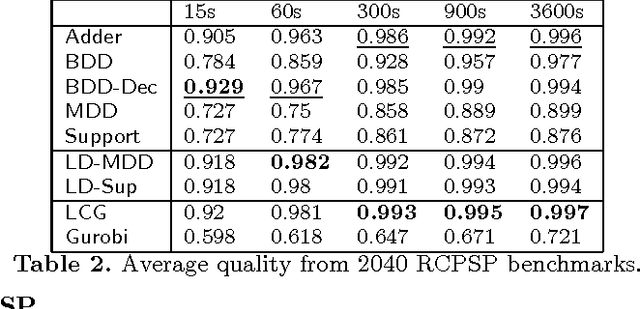
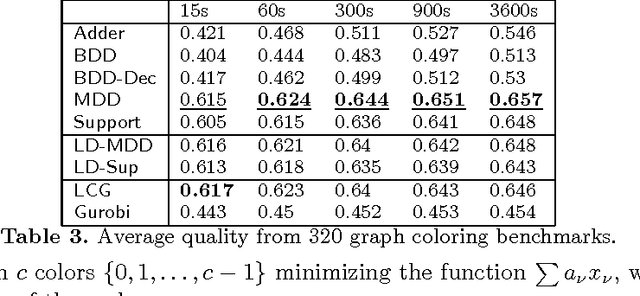
Linear integer constraints are one of the most important constraints in combinatorial problems since they are commonly found in many practical applications. Typically, encodings to Boolean satisfiability (SAT) format of conjunctive normal form perform poorly in problems with these constraints in comparison with SAT modulo theories (SMT), lazy clause generation (LCG) or mixed integer programming (MIP) solvers. In this paper we explore and categorize SAT encodings for linear integer constraints. We define new SAT encodings based on multi-valued decision diagrams, and sorting networks. We compare different SAT encodings of linear constraints and demonstrate where one may be preferable to another. We also compare SAT encodings against other solving methods and show they can be better than linear integer (MIP) solvers and sometimes better than LCG or SMT solvers on appropriate problems. Combining the new encoding with lazy decomposition, which during runtime only encodes constraints that are important to the solving process that occurs, gives the best option for many highly combinatorial problems involving linear constraints.