Beginning with You: Perceptual-Initialization Improves Vision-Language Representation and Alignment

We introduce Perceptual-Initialization (PI), a paradigm shift in visual representation learning that incorporates human perceptual structure during the initialization phase rather than as a downstream fine-tuning step. By integrating human-derived triplet embeddings from the NIGHTS dataset to initialize a CLIP vision encoder, followed by self-supervised learning on YFCC15M, our approach demonstrates significant zero-shot performance improvements, without any task-specific fine-tuning, across 29 zero shot classification and 2 retrieval benchmarks. On ImageNet-1K, zero-shot gains emerge after approximately 15 epochs of pretraining. Benefits are observed across datasets of various scales, with improvements manifesting at different stages of the pretraining process depending on dataset characteristics. Our approach consistently enhances zero-shot top-1 accuracy, top-5 accuracy, and retrieval recall (e.g., R@1, R@5) across these diverse evaluation tasks, without requiring any adaptation to target domains. These findings challenge the conventional wisdom of using human-perceptual data primarily for fine-tuning and demonstrate that embedding human perceptual structure during early representation learning yields more capable and vision-language aligned systems that generalize immediately to unseen tasks. Our work shows that "beginning with you", starting with human perception, provides a stronger foundation for general-purpose vision-language intelligence.

Dynamic Replanning for Improved Public Transport Routing

Delays in public transport are common, often impacting users through prolonged travel times and missed transfers. Existing solutions for handling delays remain limited; backup plans based on historical data miss opportunities for earlier arrivals, while snapshot planning accounts for current delays but not future ones. With the growing availability of live delay data, users can adjust their journeys in real-time. However, the literature lacks a framework that fully exploits this advantage for system-scale dynamic replanning. To address this, we formalise the dynamic replanning problem in public transport routing and propose two solutions: a "pull" approach, where users manually request replanning, and a novel "push" approach, where the server proactively monitors and adjusts journeys. Our experiments show that the push approach outperforms the pull approach, achieving significant speedups. The results also reveal substantial arrival time savings enabled by dynamic replanning.

Shifting Attention to You: Personalized Brain-Inspired AI Models

The integration of human and artificial intelligence represents a scientific opportunity to advance our understanding of information processing, as each system offers unique computational insights that can enhance and inform the other. The synthesis of human cognitive principles with artificial intelligence has the potential to produce more interpretable and functionally aligned computational models, while simultaneously providing a formal framework for investigating the neural mechanisms underlying perception, learning, and decision-making through systematic model comparisons and representational analyses. In this study, we introduce personalized brain-inspired modeling that integrates human behavioral embeddings and neural data to align with cognitive processes. We took a stepwise approach, fine-tuning the Contrastive Language-Image Pre-training (CLIP) model with large-scale behavioral decisions, group-level neural data, and finally, participant-level neural data within a broader framework that we have named CLIP-Human-Based Analysis (CLIP-HBA). We found that fine-tuning on behavioral data enhances its ability to predict human similarity judgments while indirectly aligning it with dynamic representations captured via MEG. To further gain mechanistic insights into the temporal evolution of cognitive processes, we introduced a model specifically fine-tuned on millisecond-level MEG neural dynamics (CLIP-HBA-MEG). This model resulted in enhanced temporal alignment with human neural processing while still showing improvement on behavioral alignment. Finally, we trained individualized models on participant-specific neural data, effectively capturing individualized neural dynamics and highlighting the potential for personalized AI systems. These personalized systems have far-reaching implications for the fields of medicine, cognitive research, human-computer interfaces, and AI development.

The Neighbours' Similar Fitness Property for Local Search

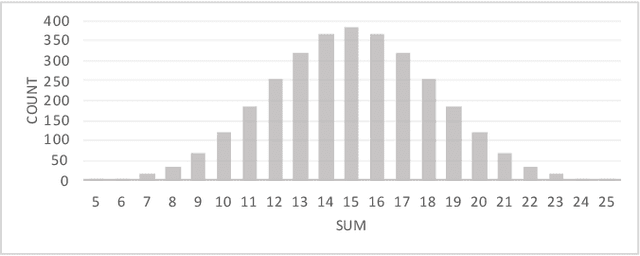
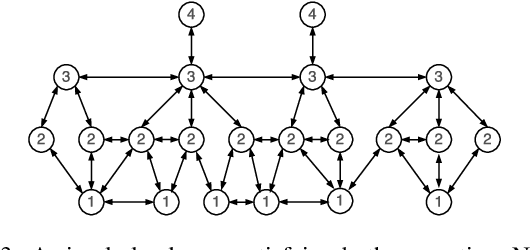
For most practical optimisation problems local search outperforms random sampling - despite the "No Free Lunch Theorem". This paper introduces a property of search landscapes termed Neighbours' Similar Fitness (NSF) that underlies the good performance of neighbourhood search in terms of local improvement. Though necessary, NSF is not sufficient to ensure that searching for improvement among the neighbours of a good solution is better than random search. The paper introduces an additional (natural) property which supports a general proof that, for NSF landscapes, neighbourhood search beats random search.

Is perturbation an effective restart strategy?

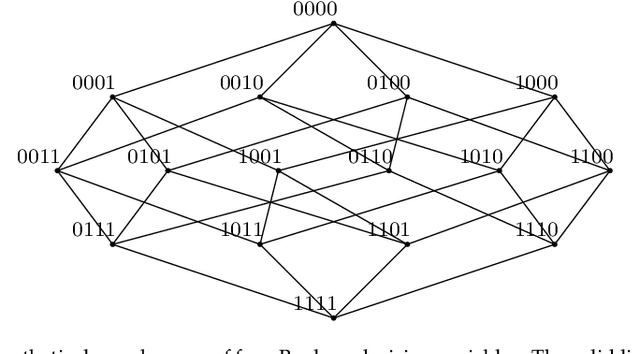
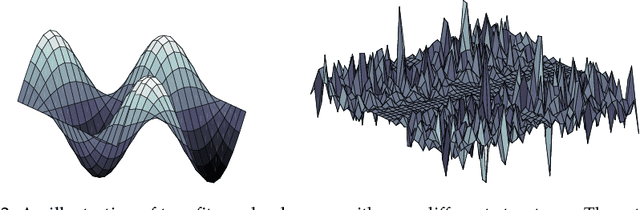
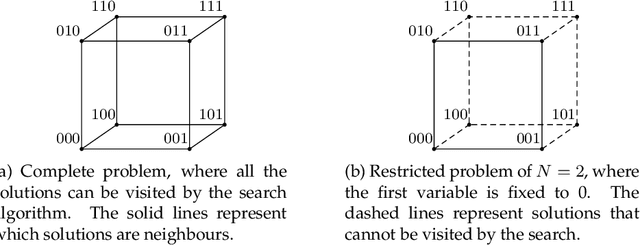
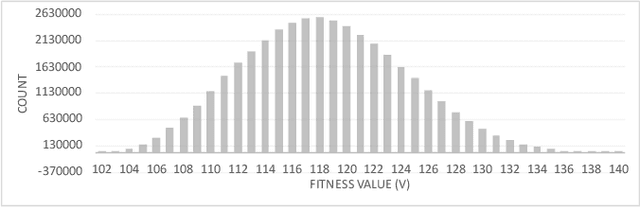
Premature convergence can be detrimental to the performance of search methods, which is why many search algorithms include restart strategies to deal with it. While it is common to perturb the incumbent solution with diversification steps of various sizes with the hope that the search method will find a new basin of attraction leading to a better local optimum, it is usually not clear how big the perturbation step should be. We introduce a new property of fitness landscapes termed "Neighbours with Similar Fitness" and we demonstrate that the effectiveness of a restart strategy depends on this property.

Steepest ascent can be exponential in bounded treewidth problems

We investigate the complexity of local search based on steepest ascent. We show that even when all variables have domains of size two and the underlying constraint graph of variable interactions has bounded treewidth (in our construction, treewidth 7), there are fitness landscapes for which an exponential number of steps may be required to reach a local optimum. This is an improvement on prior recursive constructions of long steepest ascents, which we prove to need constraint graphs of unbounded treewidth.