Steepest ascent can be exponential in bounded treewidth problems

We investigate the complexity of local search based on steepest ascent. We show that even when all variables have domains of size two and the underlying constraint graph of variable interactions has bounded treewidth (in our construction, treewidth 7), there are fitness landscapes for which an exponential number of steps may be required to reach a local optimum. This is an improvement on prior recursive constructions of long steepest ascents, which we prove to need constraint graphs of unbounded treewidth.

On Singleton Arc Consistency for CSPs Defined by Monotone Patterns

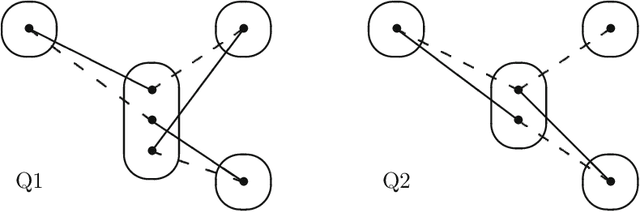
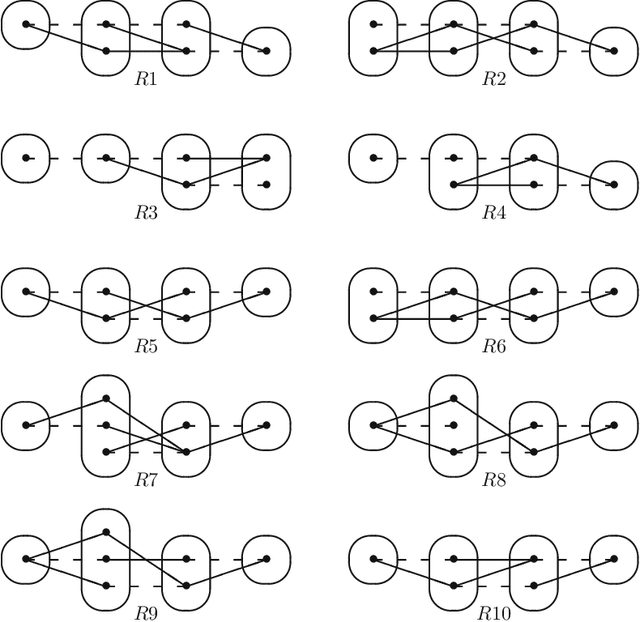
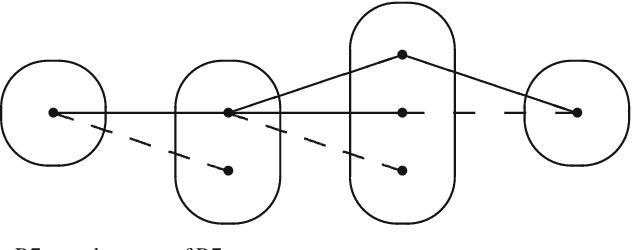
Singleton arc consistency is an important type of local consistency which has been recently shown to solve all constraint satisfaction problems (CSPs) over constraint languages of bounded width. We aim to characterise all classes of CSPs defined by a forbidden pattern that are solved by singleton arc consistency and closed under removing constraints. We identify five new patterns whose absence ensures solvability by singleton arc consistency, four of which are provably maximal and three of which generalise 2-SAT. Combined with simple counter-examples for other patterns, we make significant progress towards a complete classification.

Variable and value elimination in binary constraint satisfaction via forbidden patterns

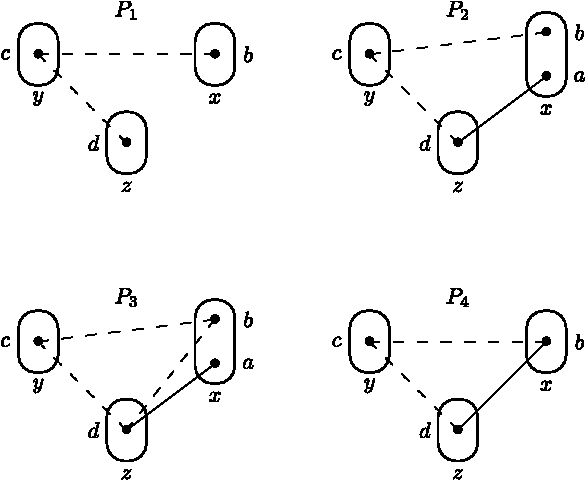
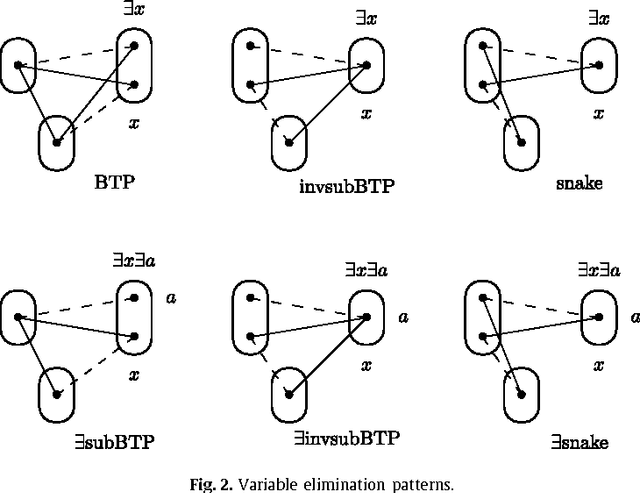
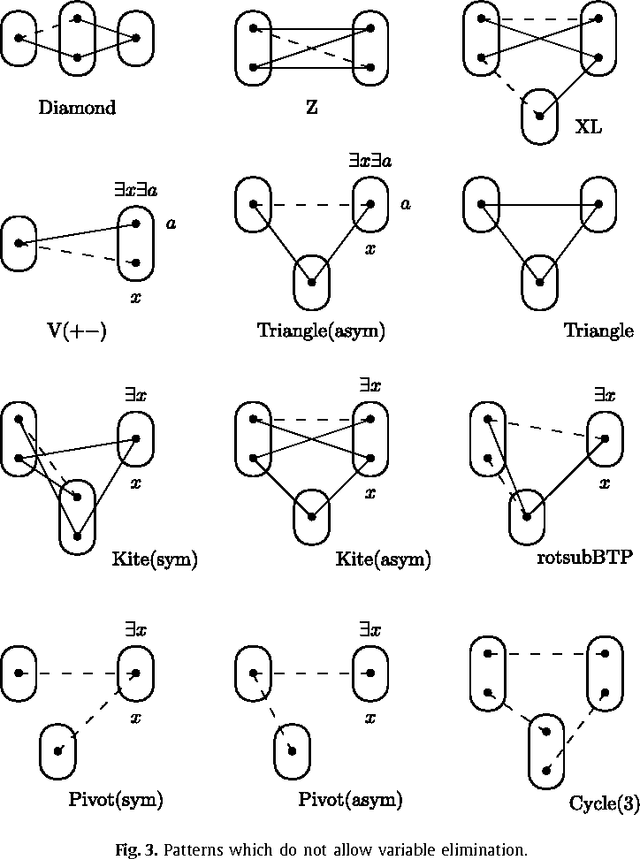
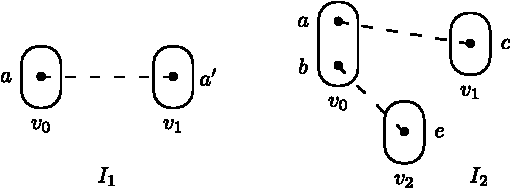
Variable or value elimination in a constraint satisfaction problem (CSP) can be used in preprocessing or during search to reduce search space size. A variable elimination rule (value elimination rule) allows the polynomial-time identification of certain variables (domain elements) whose elimination, without the introduction of extra compensatory constraints, does not affect the satisfiability of an instance. We show that there are essentially just four variable elimination rules and three value elimination rules defined by forbidding generic sub-instances, known as irreducible existential patterns, in arc-consistent CSP instances. One of the variable elimination rules is the already-known Broken Triangle Property, whereas the other three are novel. The three value elimination rules can all be seen as strict generalisations of neighbourhood substitution.

The tractability of CSP classes defined by forbidden patterns

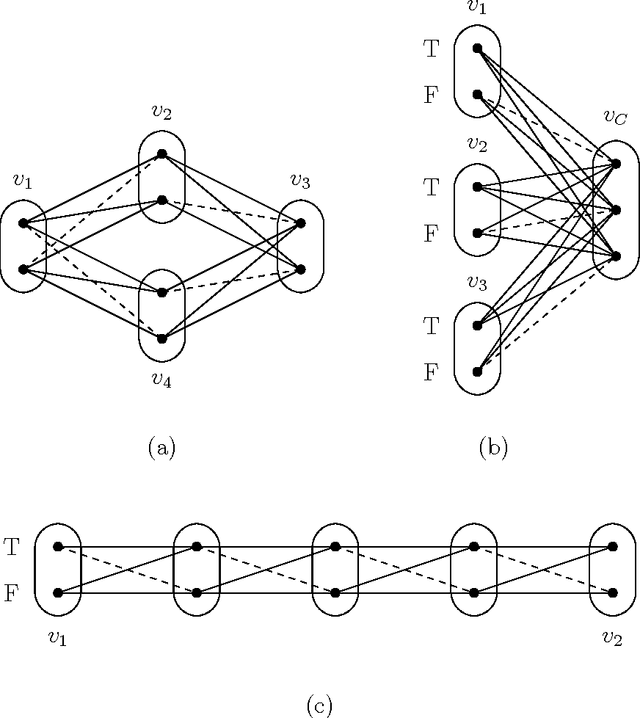
The constraint satisfaction problem (CSP) is a general problem central to computer science and artificial intelligence. Although the CSP is NP-hard in general, considerable effort has been spent on identifying tractable subclasses. The main two approaches consider structural properties (restrictions on the hypergraph of constraint scopes) and relational properties (restrictions on the language of constraint relations). Recently, some authors have considered hybrid properties that restrict the constraint hypergraph and the relations simultaneously. Our key contribution is the novel concept of a CSP pattern and classes of problems defined by forbidden patterns (which can be viewed as forbidding generic subproblems). We describe the theoretical framework which can be used to reason about classes of problems defined by forbidden patterns. We show that this framework generalises relational properties and allows us to capture known hybrid tractable classes. Although we are not close to obtaining a dichotomy concerning the tractability of general forbidden patterns, we are able to make some progress in a special case: classes of problems that arise when we can only forbid binary negative patterns (generic subproblems in which only inconsistent tuples are specified). In this case we are able to characterise very large classes of tractable and NP-hard forbidden patterns. This leaves the complexity of just one case unresolved and we conjecture that this last case is tractable.

Tractable Combinations of Global Constraints

We study the complexity of constraint satisfaction problems involving global constraints, i.e., special-purpose constraints provided by a solver and represented implicitly by a parametrised algorithm. Such constraints are widely used; indeed, they are one of the key reasons for the success of constraint programming in solving real-world problems. Previous work has focused on the development of efficient propagators for individual constraints. In this paper, we identify a new tractable class of constraint problems involving global constraints of unbounded arity. To do so, we combine structural restrictions with the observation that some important types of global constraint do not distinguish between large classes of equivalent solutions.

The Expressive Power of Binary Submodular Functions

It has previously been an open problem whether all Boolean submodular functions can be decomposed into a sum of binary submodular functions over a possibly larger set of variables. This problem has been considered within several different contexts in computer science, including computer vision, artificial intelligence, and pseudo-Boolean optimisation. Using a connection between the expressive power of valued constraints and certain algebraic properties of functions, we answer this question negatively. Our results have several corollaries. First, we characterise precisely which submodular functions of arity 4 can be expressed by binary submodular functions. Next, we identify a novel class of submodular functions of arbitrary arities which can be expressed by binary submodular functions, and therefore minimised efficiently using a so-called expressibility reduction to the Min-Cut problem. More importantly, our results imply limitations on this kind of reduction and establish for the first time that it cannot be used in general to minimise arbitrary submodular functions. Finally, we refute a conjecture of Promislow and Young on the structure of the extreme rays of the cone of Boolean submodular functions.