Directed Graph Embeddings in Pseudo-Riemannian Manifolds

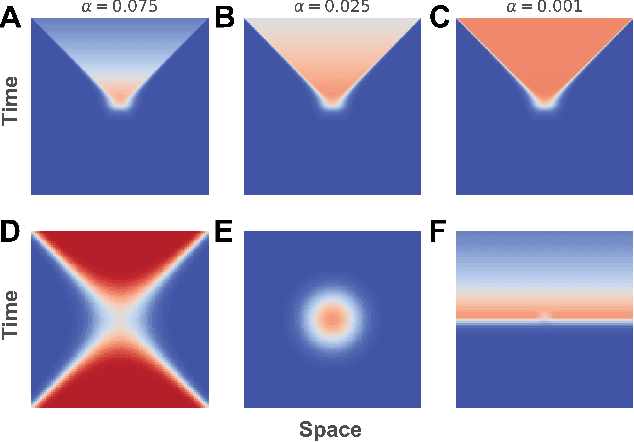
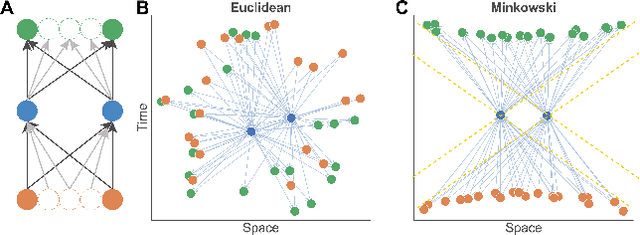
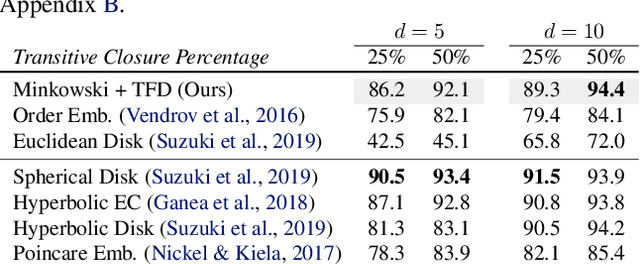
The inductive biases of graph representation learning algorithms are often encoded in the background geometry of their embedding space. In this paper, we show that general directed graphs can be effectively represented by an embedding model that combines three components: a pseudo-Riemannian metric structure, a non-trivial global topology, and a unique likelihood function that explicitly incorporates a preferred direction in embedding space. We demonstrate the representational capabilities of this method by applying it to the task of link prediction on a series of synthetic and real directed graphs from natural language applications and biology. In particular, we show that low-dimensional cylindrical Minkowski and anti-de Sitter spacetimes can produce equal or better graph representations than curved Riemannian manifolds of higher dimensions.

Contrastive Mixture of Posteriors for Counterfactual Inference, Data Integration and Fairness

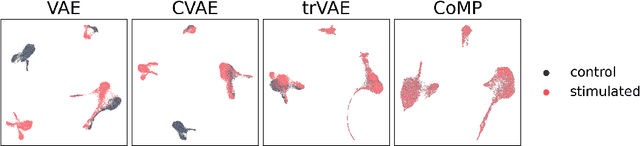
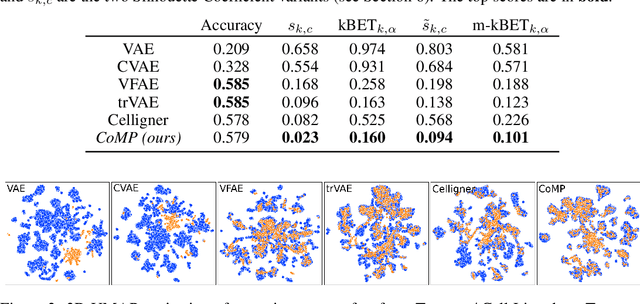
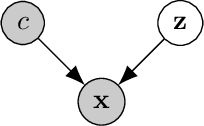
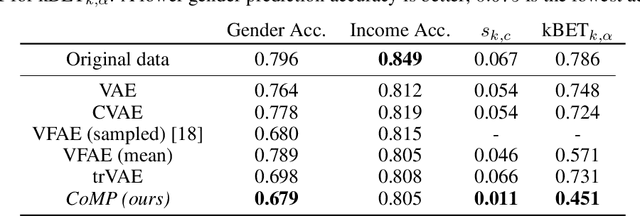
Learning meaningful representations of data that can address challenges such as batch effect correction, data integration and counterfactual inference is a central problem in many domains including computational biology. Adopting a Conditional VAE framework, we identify the mathematical principle that unites these challenges: learning a representation that is marginally independent of a condition variable. We therefore propose the Contrastive Mixture of Posteriors (CoMP) method that uses a novel misalignment penalty to enforce this independence. This penalty is defined in terms of mixtures of the variational posteriors themselves, unlike prior work which uses external discrepancy measures such as MMD to ensure independence in latent space. We show that CoMP has attractive theoretical properties compared to previous approaches, especially when there is complex global structure in latent space. We further demonstrate state of the art performance on a number of real-world problems, including the challenging tasks of aligning human tumour samples with cancer cell-lines and performing counterfactual inference on single-cell RNA sequencing data. Incidentally, we find parallels with the fair representation learning literature, and demonstrate CoMP has competitive performance in learning fair yet expressive latent representations.

The tractability of CSP classes defined by forbidden patterns

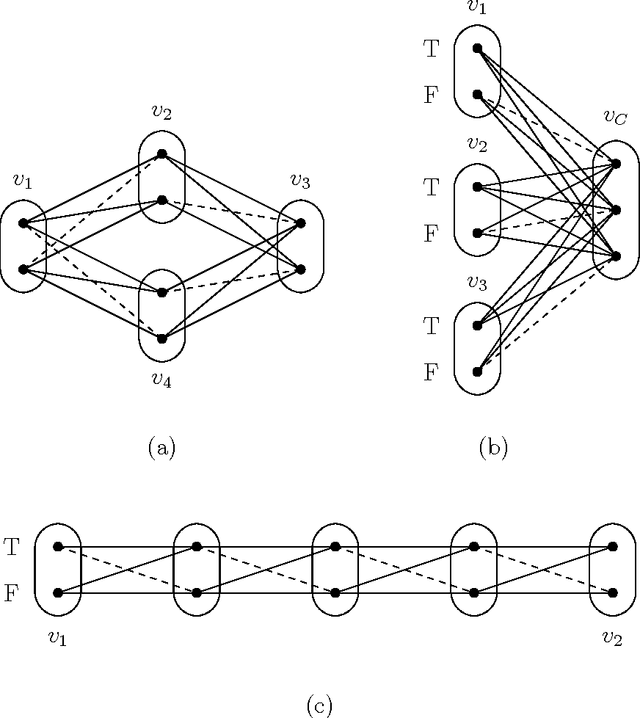
The constraint satisfaction problem (CSP) is a general problem central to computer science and artificial intelligence. Although the CSP is NP-hard in general, considerable effort has been spent on identifying tractable subclasses. The main two approaches consider structural properties (restrictions on the hypergraph of constraint scopes) and relational properties (restrictions on the language of constraint relations). Recently, some authors have considered hybrid properties that restrict the constraint hypergraph and the relations simultaneously. Our key contribution is the novel concept of a CSP pattern and classes of problems defined by forbidden patterns (which can be viewed as forbidding generic subproblems). We describe the theoretical framework which can be used to reason about classes of problems defined by forbidden patterns. We show that this framework generalises relational properties and allows us to capture known hybrid tractable classes. Although we are not close to obtaining a dichotomy concerning the tractability of general forbidden patterns, we are able to make some progress in a special case: classes of problems that arise when we can only forbid binary negative patterns (generic subproblems in which only inconsistent tuples are specified). In this case we are able to characterise very large classes of tractable and NP-hard forbidden patterns. This leaves the complexity of just one case unresolved and we conjecture that this last case is tractable.