Proxy-based Zero-Shot Entity Linking by Effective Candidate Retrieval

A recent advancement in the domain of biomedical Entity Linking is the development of powerful two-stage algorithms, an initial candidate retrieval stage that generates a shortlist of entities for each mention, followed by a candidate ranking stage. However, the effectiveness of both stages are inextricably dependent on computationally expensive components. Specifically, in candidate retrieval via dense representation retrieval it is important to have hard negative samples, which require repeated forward passes and nearest neighbour searches across the entire entity label set throughout training. In this work, we show that pairing a proxy-based metric learning loss with an adversarial regularizer provides an efficient alternative to hard negative sampling in the candidate retrieval stage. In particular, we show competitive performance on the recall@1 metric, thereby providing the option to leave out the expensive candidate ranking step. Finally, we demonstrate how the model can be used in a zero-shot setting to discover out of knowledge base biomedical entities.

Pseudo-Riemannian Embedding Models for Multi-Relational Graph Representations

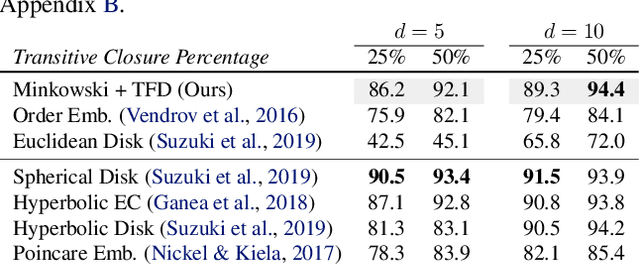
In this paper we generalize single-relation pseudo-Riemannian graph embedding models to multi-relational networks, and show that the typical approach of encoding relations as manifold transformations translates from the Riemannian to the pseudo-Riemannian case. In addition we construct a view of relations as separate spacetime submanifolds of multi-time manifolds, and consider an interpolation between a pseudo-Riemannian embedding model and its Wick-rotated Riemannian counterpart. We validate these extensions in the task of link prediction, focusing on flat Lorentzian manifolds, and demonstrate their use in both knowledge graph completion and knowledge discovery in a biological domain.

Directed Graph Embeddings in Pseudo-Riemannian Manifolds

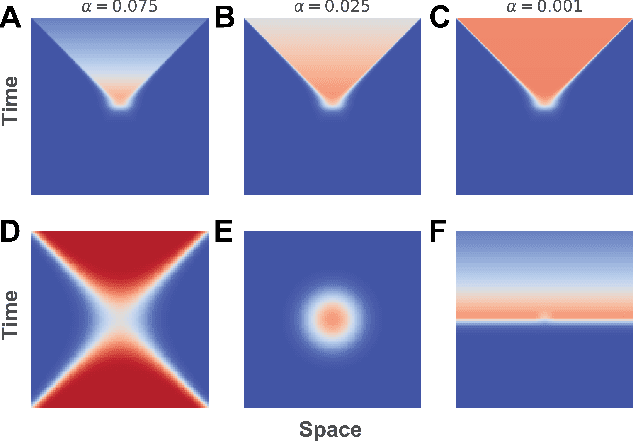
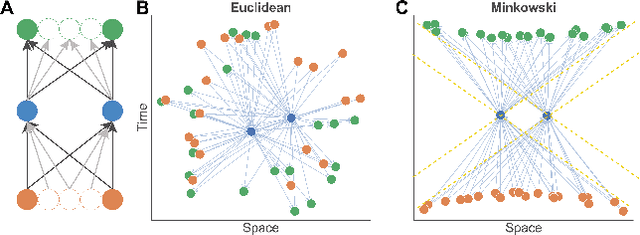
The inductive biases of graph representation learning algorithms are often encoded in the background geometry of their embedding space. In this paper, we show that general directed graphs can be effectively represented by an embedding model that combines three components: a pseudo-Riemannian metric structure, a non-trivial global topology, and a unique likelihood function that explicitly incorporates a preferred direction in embedding space. We demonstrate the representational capabilities of this method by applying it to the task of link prediction on a series of synthetic and real directed graphs from natural language applications and biology. In particular, we show that low-dimensional cylindrical Minkowski and anti-de Sitter spacetimes can produce equal or better graph representations than curved Riemannian manifolds of higher dimensions.

Contrastive Mixture of Posteriors for Counterfactual Inference, Data Integration and Fairness

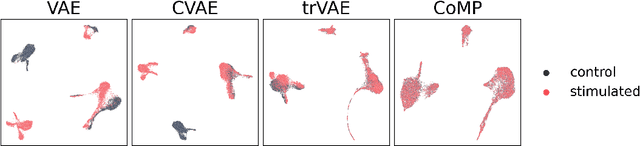
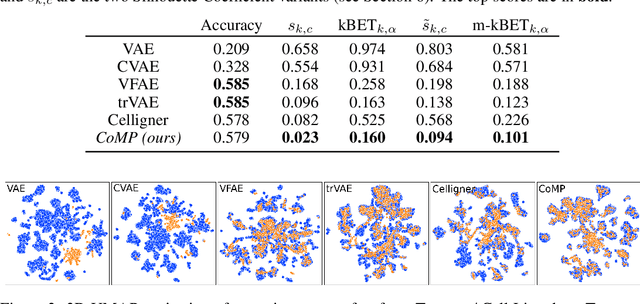
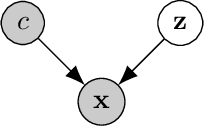
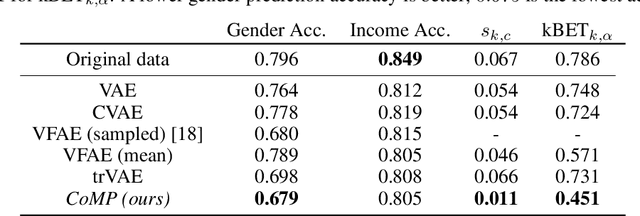
Learning meaningful representations of data that can address challenges such as batch effect correction, data integration and counterfactual inference is a central problem in many domains including computational biology. Adopting a Conditional VAE framework, we identify the mathematical principle that unites these challenges: learning a representation that is marginally independent of a condition variable. We therefore propose the Contrastive Mixture of Posteriors (CoMP) method that uses a novel misalignment penalty to enforce this independence. This penalty is defined in terms of mixtures of the variational posteriors themselves, unlike prior work which uses external discrepancy measures such as MMD to ensure independence in latent space. We show that CoMP has attractive theoretical properties compared to previous approaches, especially when there is complex global structure in latent space. We further demonstrate state of the art performance on a number of real-world problems, including the challenging tasks of aligning human tumour samples with cancer cell-lines and performing counterfactual inference on single-cell RNA sequencing data. Incidentally, we find parallels with the fair representation learning literature, and demonstrate CoMP has competitive performance in learning fair yet expressive latent representations.

Interpretable Graph Convolutional Neural Networks for Inference on Noisy Knowledge Graphs

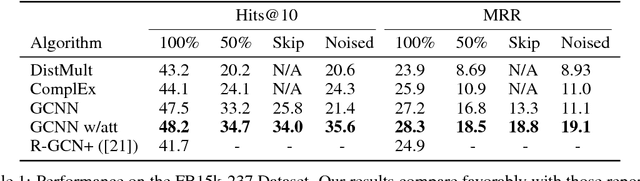
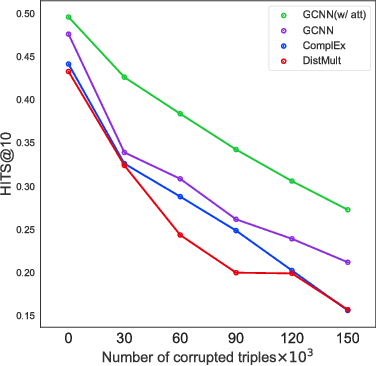
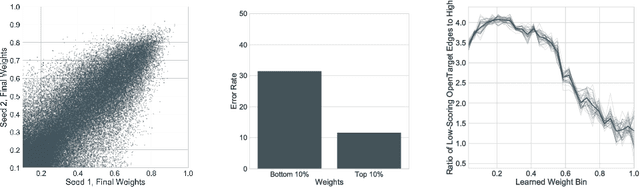
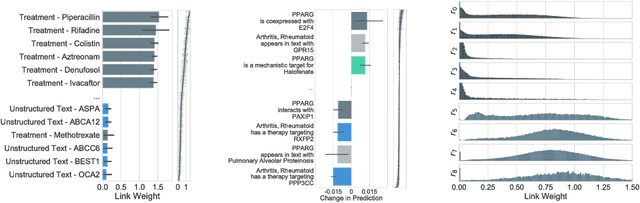
In this work, we provide a new formulation for Graph Convolutional Neural Networks (GCNNs) for link prediction on graph data that addresses common challenges for biomedical knowledge graphs (KGs). We introduce a regularized attention mechanism to GCNNs that not only improves performance on clean datasets, but also favorably accommodates noise in KGs, a pervasive issue in real-world applications. Further, we explore new visualization methods for interpretable modelling and to illustrate how the learned representation can be exploited to automate dataset denoising. The results are demonstrated on a synthetic dataset, the common benchmark dataset FB15k-237, and a large biomedical knowledge graph derived from a combination of noisy and clean data sources. Using these improvements, we visualize a learned model's representation of the disease cystic fibrosis and demonstrate how to interrogate a neural network to show the potential of PPARG as a candidate therapeutic target for rheumatoid arthritis.

Random Forests on Distance Matrices for Imaging Genetics Studies

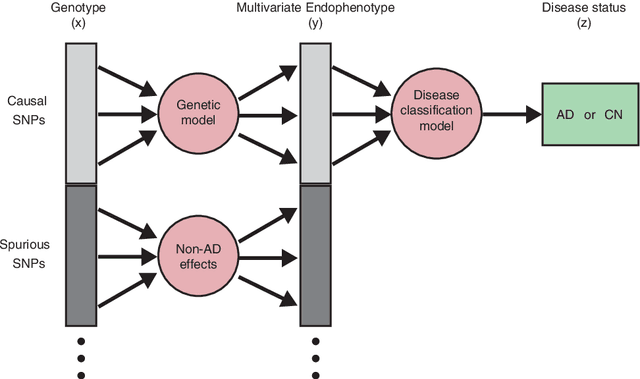
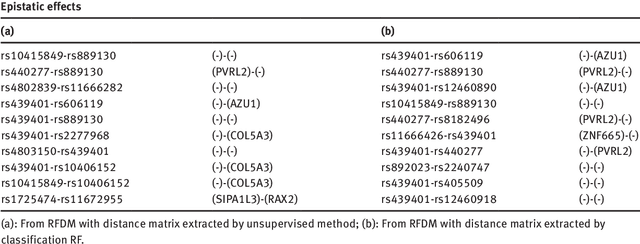
We propose a non-parametric regression methodology, Random Forests on Distance Matrices (RFDM), for detecting genetic variants associated to quantitative phenotypes representing the human brain's structure or function, and obtained using neuroimaging techniques. RFDM, which is an extension of decision forests, requires a distance matrix as response that encodes all pair-wise phenotypic distances in the random sample. We discuss ways to learn such distances directly from the data using manifold learning techniques, and how to define such distances when the phenotypes are non-vectorial objects such as brain connectivity networks. We also describe an extension of RFDM to detect espistatic effects while keeping the computational complexity low. Extensive simulation results and an application to an imaging genetics study of Alzheimer's Disease are presented and discussed.