Proxy-based Zero-Shot Entity Linking by Effective Candidate Retrieval

A recent advancement in the domain of biomedical Entity Linking is the development of powerful two-stage algorithms, an initial candidate retrieval stage that generates a shortlist of entities for each mention, followed by a candidate ranking stage. However, the effectiveness of both stages are inextricably dependent on computationally expensive components. Specifically, in candidate retrieval via dense representation retrieval it is important to have hard negative samples, which require repeated forward passes and nearest neighbour searches across the entire entity label set throughout training. In this work, we show that pairing a proxy-based metric learning loss with an adversarial regularizer provides an efficient alternative to hard negative sampling in the candidate retrieval stage. In particular, we show competitive performance on the recall@1 metric, thereby providing the option to leave out the expensive candidate ranking step. Finally, we demonstrate how the model can be used in a zero-shot setting to discover out of knowledge base biomedical entities.

Coupling weak and strong supervision for classification of prostate cancer histopathology images

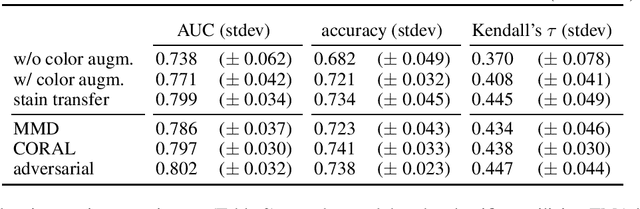
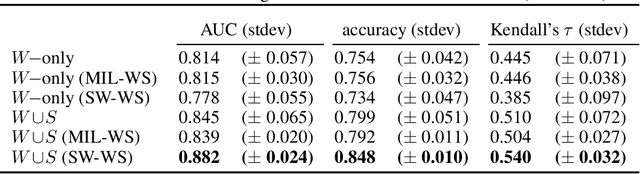
Automated grading of prostate cancer histopathology images is a challenging task, with one key challenge being the scarcity of annotations down to the level of regions of interest (strong labels), as typically the prostate cancer Gleason score is known only for entire tissue slides (weak labels). In this study, we focus on automated Gleason score assignment of prostate cancer whole-slide images on the basis of a large weakly-labeled dataset and a smaller strongly-labeled one. We efficiently leverage information from both label sources by jointly training a classifier on the two datasets and by introducing a gradient update scheme that assigns different relative importances to each training example, as a means of self-controlling the weak supervision signal. Our approach achieves superior performance when compared with standard Gleason scoring methods.

Markov Network Structure Learning via Ensemble-of-Forests Models

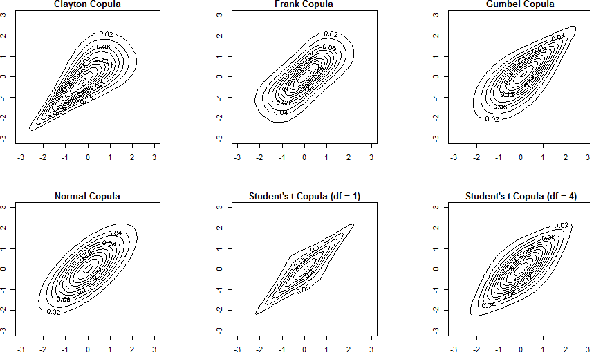
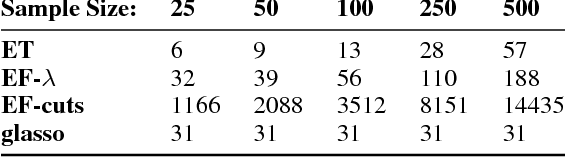
Real world systems typically feature a variety of different dependency types and topologies that complicate model selection for probabilistic graphical models. We introduce the ensemble-of-forests model, a generalization of the ensemble-of-trees model. Our model enables structure learning of Markov random fields (MRF) with multiple connected components and arbitrary potentials. We present two approximate inference techniques for this model and demonstrate their performance on synthetic data. Our results suggest that the ensemble-of-forests approach can accurately recover sparse, possibly disconnected MRF topologies, even in presence of non-Gaussian dependencies and/or low sample size. We applied the ensemble-of-forests model to learn the structure of perturbed signaling networks of immune cells and found that these frequently exhibit non-Gaussian dependencies with disconnected MRF topologies. In summary, we expect that the ensemble-of-forests model will enable MRF structure learning in other high dimensional real world settings that are governed by non-trivial dependencies.