Markov Network Structure Learning via Ensemble-of-Forests Models
Paper and Code
Dec 17, 2013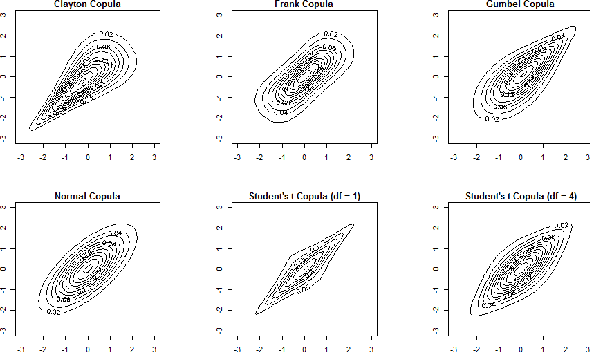
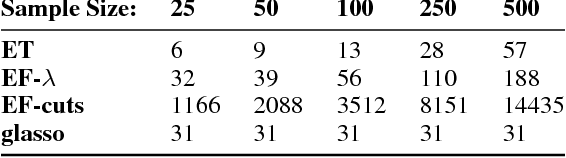


Real world systems typically feature a variety of different dependency types and topologies that complicate model selection for probabilistic graphical models. We introduce the ensemble-of-forests model, a generalization of the ensemble-of-trees model. Our model enables structure learning of Markov random fields (MRF) with multiple connected components and arbitrary potentials. We present two approximate inference techniques for this model and demonstrate their performance on synthetic data. Our results suggest that the ensemble-of-forests approach can accurately recover sparse, possibly disconnected MRF topologies, even in presence of non-Gaussian dependencies and/or low sample size. We applied the ensemble-of-forests model to learn the structure of perturbed signaling networks of immune cells and found that these frequently exhibit non-Gaussian dependencies with disconnected MRF topologies. In summary, we expect that the ensemble-of-forests model will enable MRF structure learning in other high dimensional real world settings that are governed by non-trivial dependencies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge