Proxy-based Zero-Shot Entity Linking by Effective Candidate Retrieval

A recent advancement in the domain of biomedical Entity Linking is the development of powerful two-stage algorithms, an initial candidate retrieval stage that generates a shortlist of entities for each mention, followed by a candidate ranking stage. However, the effectiveness of both stages are inextricably dependent on computationally expensive components. Specifically, in candidate retrieval via dense representation retrieval it is important to have hard negative samples, which require repeated forward passes and nearest neighbour searches across the entire entity label set throughout training. In this work, we show that pairing a proxy-based metric learning loss with an adversarial regularizer provides an efficient alternative to hard negative sampling in the candidate retrieval stage. In particular, we show competitive performance on the recall@1 metric, thereby providing the option to leave out the expensive candidate ranking step. Finally, we demonstrate how the model can be used in a zero-shot setting to discover out of knowledge base biomedical entities.

Pseudo-Riemannian Embedding Models for Multi-Relational Graph Representations

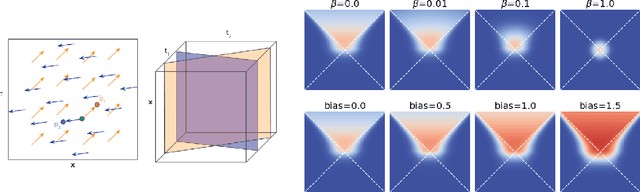
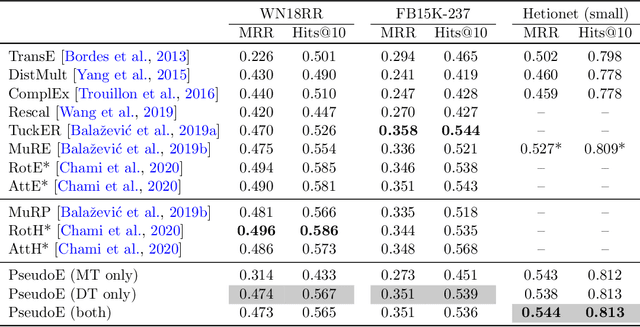
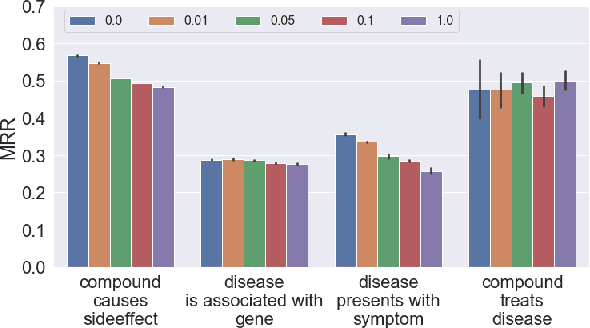
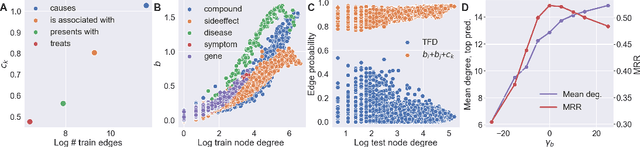
In this paper we generalize single-relation pseudo-Riemannian graph embedding models to multi-relational networks, and show that the typical approach of encoding relations as manifold transformations translates from the Riemannian to the pseudo-Riemannian case. In addition we construct a view of relations as separate spacetime submanifolds of multi-time manifolds, and consider an interpolation between a pseudo-Riemannian embedding model and its Wick-rotated Riemannian counterpart. We validate these extensions in the task of link prediction, focusing on flat Lorentzian manifolds, and demonstrate their use in both knowledge graph completion and knowledge discovery in a biological domain.

Directed Graph Embeddings in Pseudo-Riemannian Manifolds

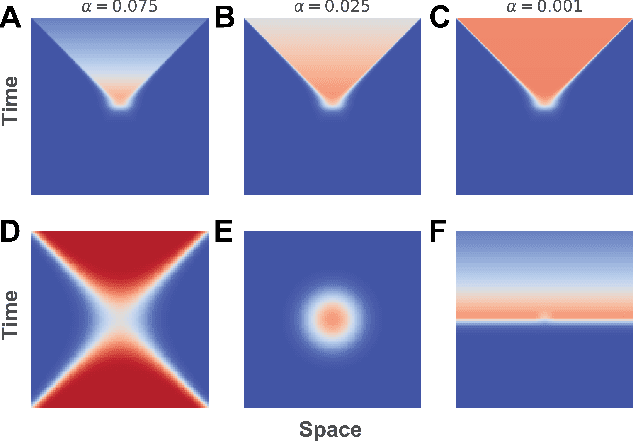
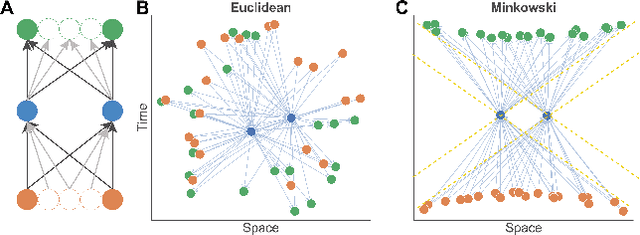
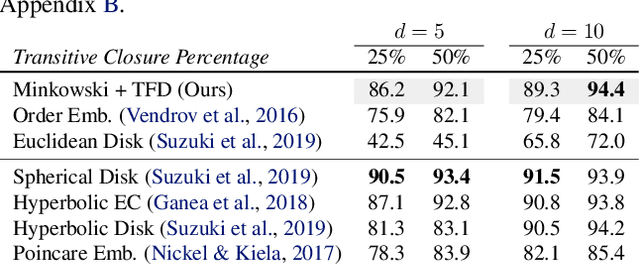
The inductive biases of graph representation learning algorithms are often encoded in the background geometry of their embedding space. In this paper, we show that general directed graphs can be effectively represented by an embedding model that combines three components: a pseudo-Riemannian metric structure, a non-trivial global topology, and a unique likelihood function that explicitly incorporates a preferred direction in embedding space. We demonstrate the representational capabilities of this method by applying it to the task of link prediction on a series of synthetic and real directed graphs from natural language applications and biology. In particular, we show that low-dimensional cylindrical Minkowski and anti-de Sitter spacetimes can produce equal or better graph representations than curved Riemannian manifolds of higher dimensions.

Stabilizing Generative Adversarial Network Training: A Survey

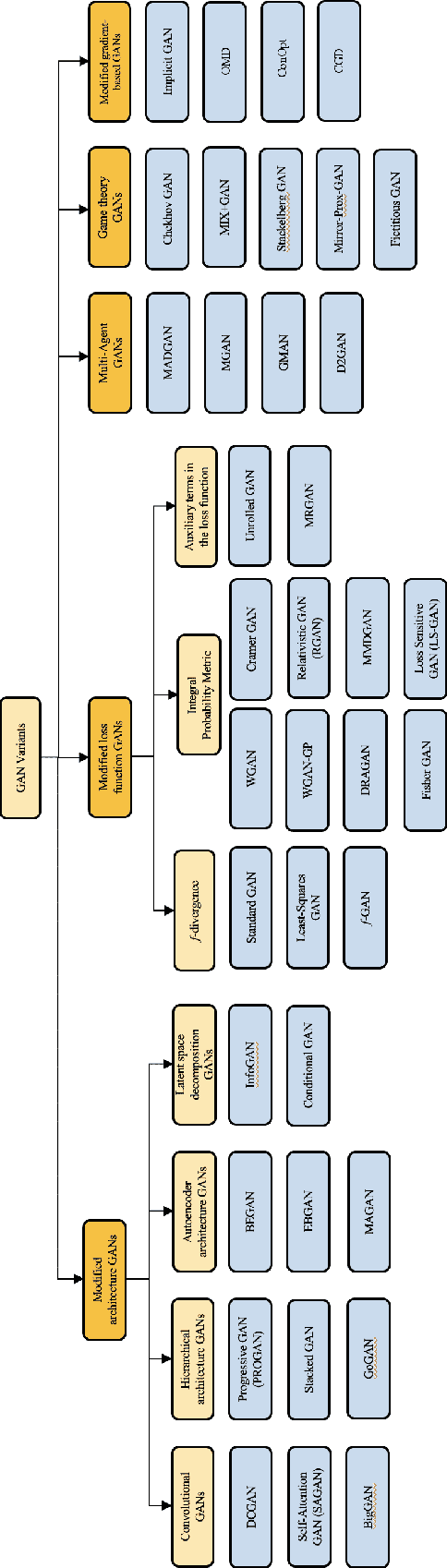
Generative Adversarial Networks (GANs) are a type of Generative Models, which received wide attention for their ability to model complex real-world data. With a considerably large number of potential applications and a promise to alleviate some of the major issues of the field of Artificial Intelligence, recent years have seen rapid progress in the field of GANs. Despite the relative success, the process of training GANs remains challenging, suffering from instability issues such as mode collapse and vanishing gradients. This survey summarizes the approaches and methods employed for the purpose of stabilizing GAN training procedure. We provide a brief explanation behind the workings of GANs and categorize employed stabilization techniques outlining each of the approaches. Finally, we discuss the advantages and disadvantages of each of the methods, offering a comparative summary of the literature on stabilizing GAN training procedure.