Random Forests on Distance Matrices for Imaging Genetics Studies
Paper and Code
Sep 24, 2013

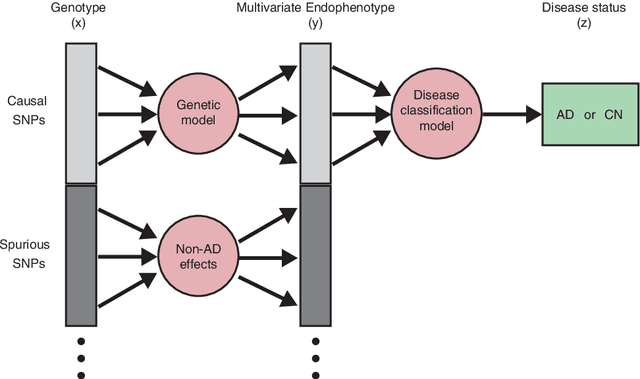
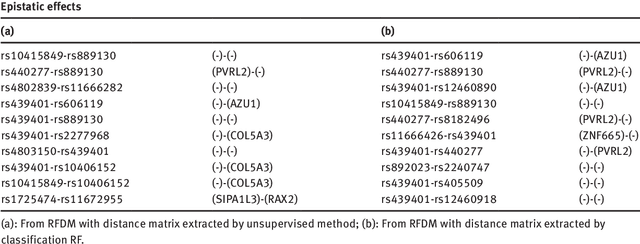
We propose a non-parametric regression methodology, Random Forests on Distance Matrices (RFDM), for detecting genetic variants associated to quantitative phenotypes representing the human brain's structure or function, and obtained using neuroimaging techniques. RFDM, which is an extension of decision forests, requires a distance matrix as response that encodes all pair-wise phenotypic distances in the random sample. We discuss ways to learn such distances directly from the data using manifold learning techniques, and how to define such distances when the phenotypes are non-vectorial objects such as brain connectivity networks. We also describe an extension of RFDM to detect espistatic effects while keeping the computational complexity low. Extensive simulation results and an application to an imaging genetics study of Alzheimer's Disease are presented and discussed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge