Generation and Prediction of Difficult Model Counting Instances

We present a way to create small yet difficult model counting instances. Our generator is highly parameterizable: the number of variables of the instances it produces, as well as their number of clauses and the number of literals in each clause, can all be set to any value. Our instances have been tested on state of the art model counters, against other difficult model counting instances, in the Model Counting Competition. The smallest unsolved instances of the competition, both in terms of number of variables and number of clauses, were ours. We also observe a peak of difficulty when fixing the number of variables and varying the number of clauses, in both random instances and instances built by our generator. Using these results, we predict the parameter values for which the hardest to count instances will occur.

Solving Logic Grid Puzzles with an Algorithm that Imitates Human Behavior

We present in this paper our solver for logic grid puzzles. The approach used by our algorithm mimics the way a human would try to solve the same problem. Every progress made during the solving process is accompanied by a detailed explanation of our program's reasoning. Since this reasoning is based on the same heuristics that a human would employ, the user can easily follow the given explanation.

Generating Difficult SAT Instances by Preventing Triangles

When creating benchmarks for SAT solvers, we need SAT instances that are easy to build but hard to solve. A recent development in the search for such methods has led to the Balanced SAT algorithm, which can create k-SAT instances with m clauses of high difficulty, for arbitrary k and m. In this paper we introduce the No-Triangle SAT algorithm, a SAT instance generator based on the cluster coefficient graph statistic. We empirically compare the two algorithms by fixing the arity and the number of variables, but varying the number of clauses. The hardest instances that we find are produced by No-Triangle SAT. Furthermore, difficult instances from No-Triangle SAT have a different number of clauses than difficult instances from Balanced SAT, potentially allowing a combination of the two methods to find hard SAT instances for a larger array of parameters.

Variable and value elimination in binary constraint satisfaction via forbidden patterns

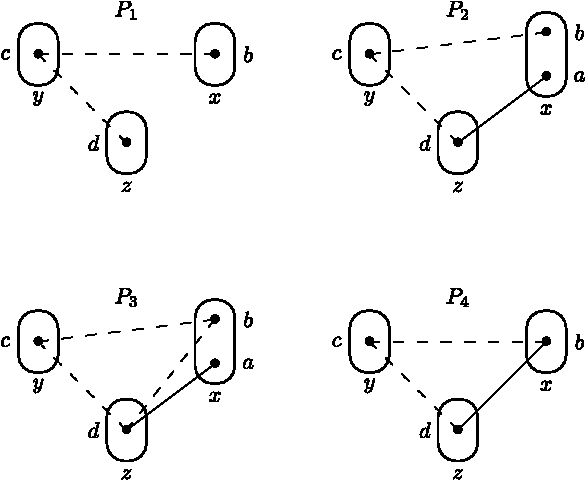
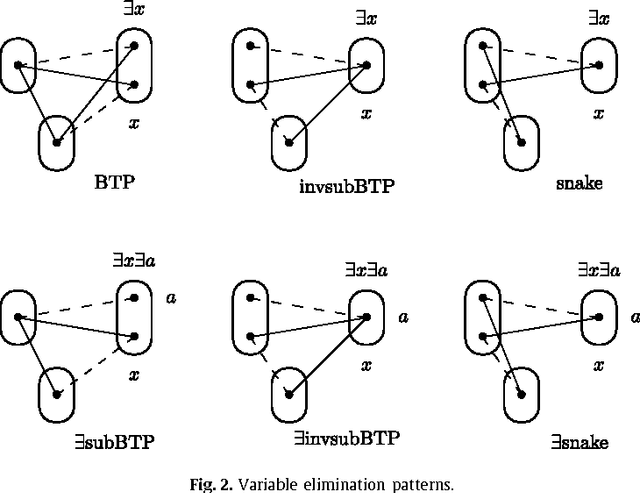
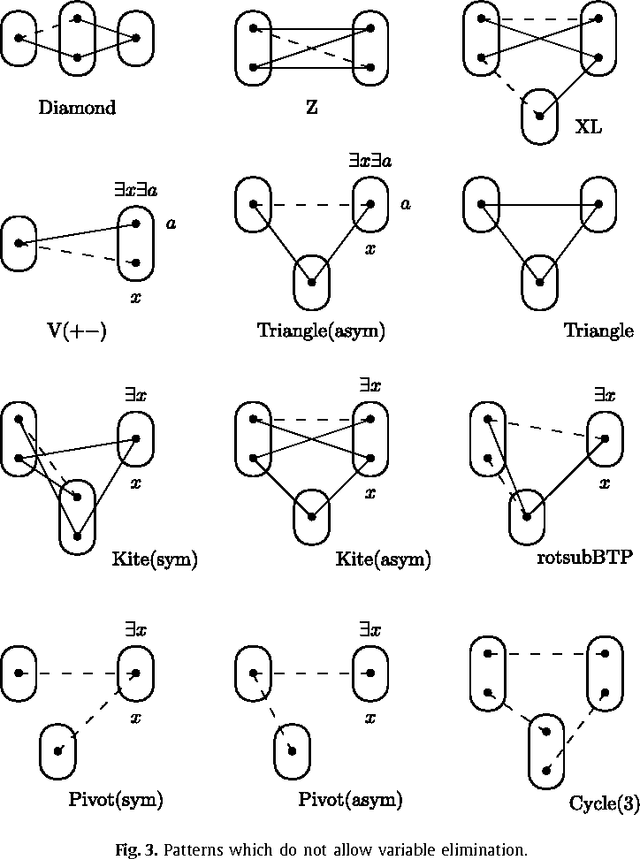
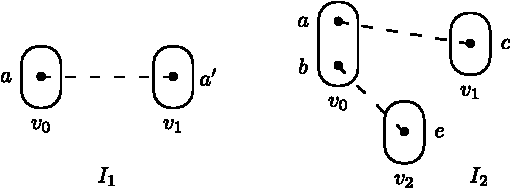
Variable or value elimination in a constraint satisfaction problem (CSP) can be used in preprocessing or during search to reduce search space size. A variable elimination rule (value elimination rule) allows the polynomial-time identification of certain variables (domain elements) whose elimination, without the introduction of extra compensatory constraints, does not affect the satisfiability of an instance. We show that there are essentially just four variable elimination rules and three value elimination rules defined by forbidding generic sub-instances, known as irreducible existential patterns, in arc-consistent CSP instances. One of the variable elimination rules is the already-known Broken Triangle Property, whereas the other three are novel. The three value elimination rules can all be seen as strict generalisations of neighbourhood substitution.

A Dichotomy for 2-Constraint Forbidden CSP Patterns

Although the CSP (constraint satisfaction problem) is NP-complete, even in the case when all constraints are binary, certain classes of instances are tractable. We study classes of instances defined by excluding subproblems. This approach has recently led to the discovery of novel tractable classes. The complete characterisation of all tractable classes defined by forbidding patterns (where a pattern is simply a compact representation of a set of subproblems) is a challenging problem. We demonstrate a dichotomy in the case of forbidden patterns consisting of either one or two constraints. This has allowed us to discover new tractable classes including, for example, a novel generalisation of 2SAT.