Clement Carbonnel
Partial Queries for Constraint Acquisition
Mar 14, 2020
Abstract:Learning constraint networks is known to require a number of membership queries exponential in the number of variables. In this paper, we learn constraint networks by asking the user partial queries. That is, we ask the user to classify assignments to subsets of the variables as positive or negative. We provide an algorithm, called QUACQ, that, given a negative example, focuses onto a constraint of the target network in a number of queries logarithmic in the size of the example. The whole constraint network can then be learned with a polynomial number of partial queries. We give information theoretic lower bounds for learning some simple classes of constraint networks and show that our generic algorithm is optimal in some cases.
On Singleton Arc Consistency for CSPs Defined by Monotone Patterns
Aug 10, 2018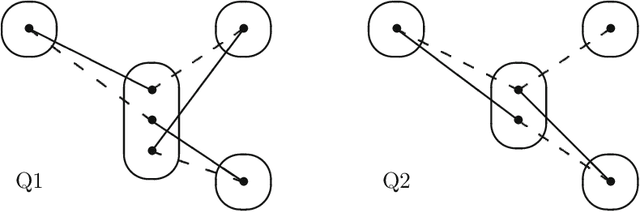
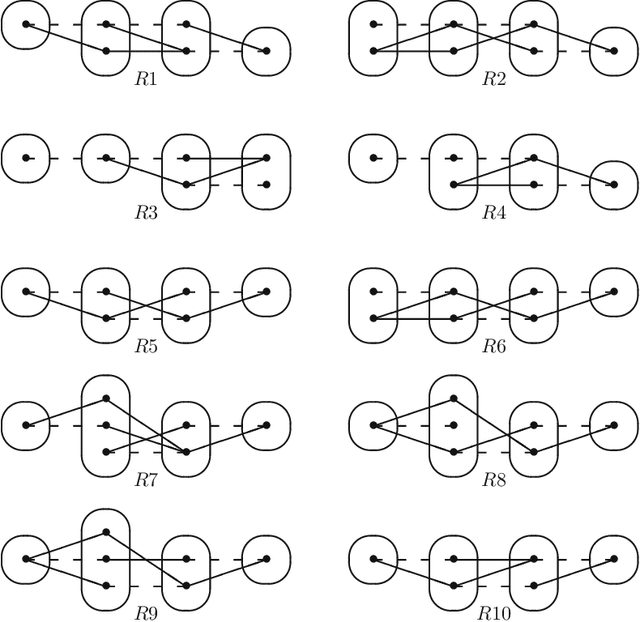
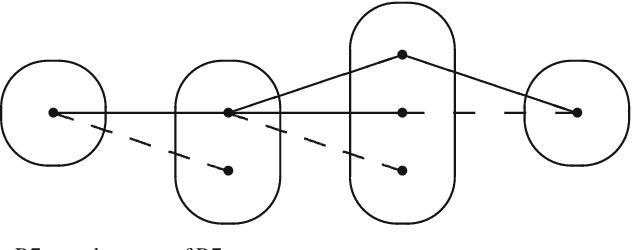

Abstract:Singleton arc consistency is an important type of local consistency which has been recently shown to solve all constraint satisfaction problems (CSPs) over constraint languages of bounded width. We aim to characterise all classes of CSPs defined by a forbidden pattern that are solved by singleton arc consistency and closed under removing constraints. We identify five new patterns whose absence ensures solvability by singleton arc consistency, four of which are provably maximal and three of which generalise 2-SAT. Combined with simple counter-examples for other patterns, we make significant progress towards a complete classification.
On Backdoors To Tractable Constraint Languages
Oct 10, 2014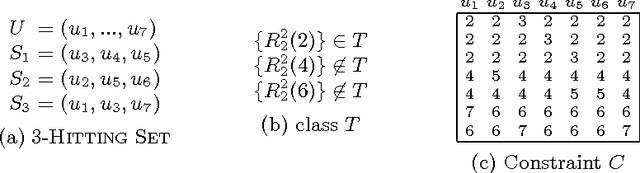
Abstract:In the context of CSPs, a strong backdoor is a subset of variables such that every complete assignment yields a residual instance guaranteed to have a specified property. If the property allows efficient solving, then a small strong backdoor provides a reasonable decomposition of the original instance into easy instances. An important challenge is the design of algorithms that can find quickly a small strong backdoor if one exists. We present a systematic study of the parameterized complexity of backdoor detection when the target property is a restricted type of constraint language defined by means of a family of polymorphisms. In particular, we show that under the weak assumption that the polymorphisms are idempotent, the problem is unlikely to be FPT when the parameter is either r (the constraint arity) or k (the size of the backdoor) unless P = NP or FPT = W[2]. When the parameter is k+r, however, we are able to identify large classes of languages for which the problem of finding a small backdoor is FPT.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge