Efficient Multiple Constraint Acquisition

Constraint acquisition systems such as QuAcq and MultiAcq can assist non-expert users to model their problems as constraint networks by classifying (partial) examples as positive or negative. For each negative example, the former focuses on one constraint of the target network, while the latter can learn a maximum number of constraints. Two bottlenecks of the acquisition process where both these algorithms encounter problems are the large number of queries required to reach convergence, and the high cpu times needed to generate queries, especially near convergence. In this paper we propose algorithmic and heuristic methods to deal with both these issues. We first describe an algorithm, called MQuAcq, that blends the main idea of MultiAcq into QuAcq resulting in a method that learns as many constraints as MultiAcq does after a negative example, but with a lower complexity. A detailed theoretical analysis of the proposed algorithm is also presented. %We also present a technique that boosts the performance of constraint acquisition by reducing the number of queries significantly. Then we turn our attention to query generation which is a significant but rather overlooked part of the acquisition process. We describe %in detail how query generation in a typical constraint acquisition system operates, and we propose heuristics for improving its efficiency. Experiments from various domains demonstrate that our resulting algorithm that integrates all the new techniques does not only generate considerably fewer queries than QuAcq and MultiAcq, but it is also by far faster than both of them, in average query generation time as well as in total run time, and also largely alleviates the premature convergence problem.

Partial Queries for Constraint Acquisition

Learning constraint networks is known to require a number of membership queries exponential in the number of variables. In this paper, we learn constraint networks by asking the user partial queries. That is, we ask the user to classify assignments to subsets of the variables as positive or negative. We provide an algorithm, called QUACQ, that, given a negative example, focuses onto a constraint of the target network in a number of queries logarithmic in the size of the example. The whole constraint network can then be learned with a polynomial number of partial queries. We give information theoretic lower bounds for learning some simple classes of constraint networks and show that our generic algorithm is optimal in some cases.

Exploiting the Pruning Power of Strong Local Consistencies Through Parallelization

Local consistencies stronger than arc consistency have received a lot of attention since the early days of CSP research. %because of the strong pruning they can achieve. However, they have not been widely adopted by CSP solvers. This is because applying such consistencies can sometimes result in considerably smaller search tree sizes and therefore in important speed-ups, but in other cases the search space reduction may be small, causing severe run time penalties. Taking advantage of recent advances in parallelization, we propose a novel approach for the application of strong local consistencies (SLCs) that can improve their performance by largely preserving the speed-ups they offer in cases where they are successful, and eliminating the run time penalties in cases where they are unsuccessful. This approach is presented in the form of two search algorithms. Both algorithms consist of a master search process, which is a typical CSP solver, and a number of slave processes, with each one implementing a SLC method. The first algorithm runs the different SLCs synchronously at each node of the search tree explored in the master process, while the second one can run them asynchronously at different nodes of the search tree. Experimental results demonstrate the benefits of the proposed method.

Experimental Evaluation of Branching Schemes for the CSP

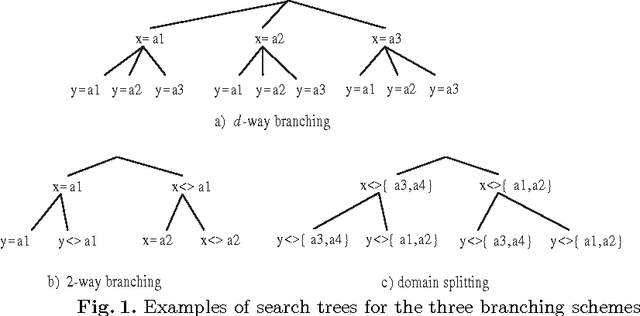
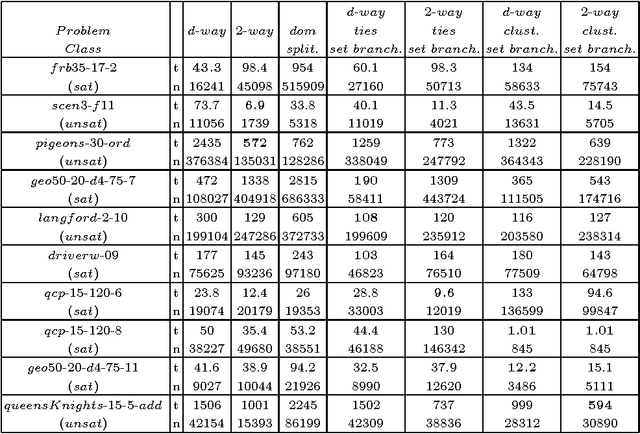
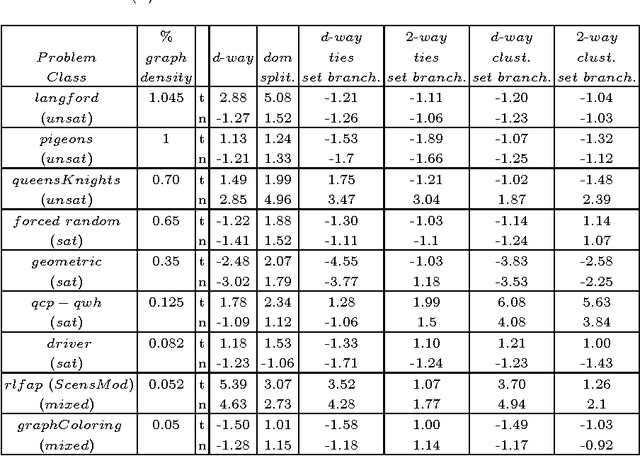
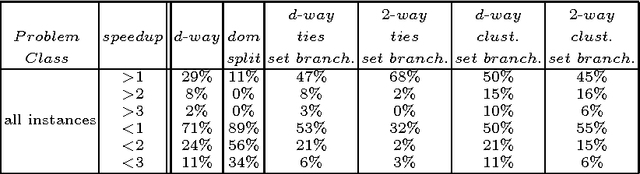
The search strategy of a CP solver is determined by the variable and value ordering heuristics it employs and by the branching scheme it follows. Although the effects of variable and value ordering heuristics on search effort have been widely studied, the effects of different branching schemes have received less attention. In this paper we study this effect through an experimental evaluation that includes standard branching schemes such as 2-way, d-way, and dichotomic domain splitting, as well as variations of set branching where branching is performed on sets of values. We also propose and evaluate a generic approach to set branching where the partition of a domain into sets is created using the scores assigned to values by a value ordering heuristic, and a clustering algorithm from machine learning. Experimental results demonstrate that although exponential differences between branching schemes, as predicted in theory between 2-way and d-way branching, are not very common, still the choice of branching scheme can make quite a difference on certain classes of problems. Set branching methods are very competitive with 2-way branching and outperform it on some problem classes. A statistical analysis of the results reveals that our generic clustering-based set branching method is the best among the methods compared.

Improving the Performance of maxRPC

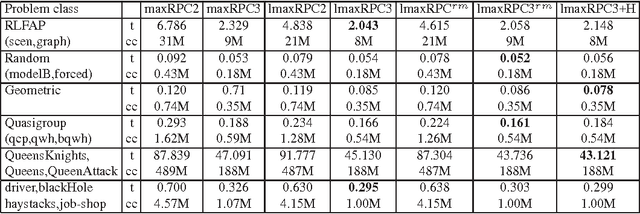
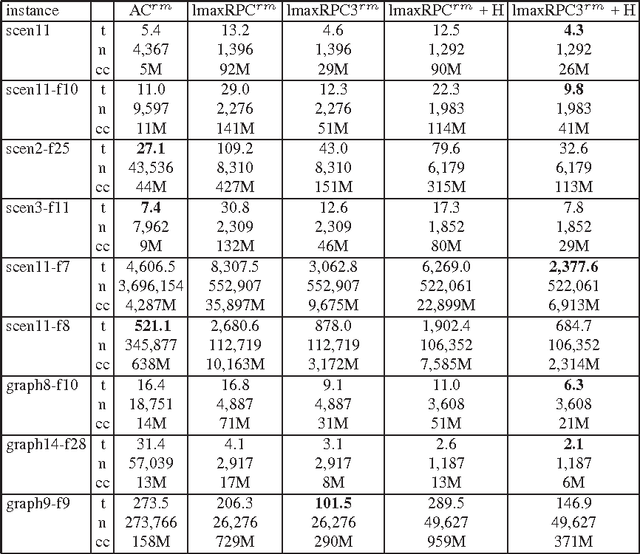
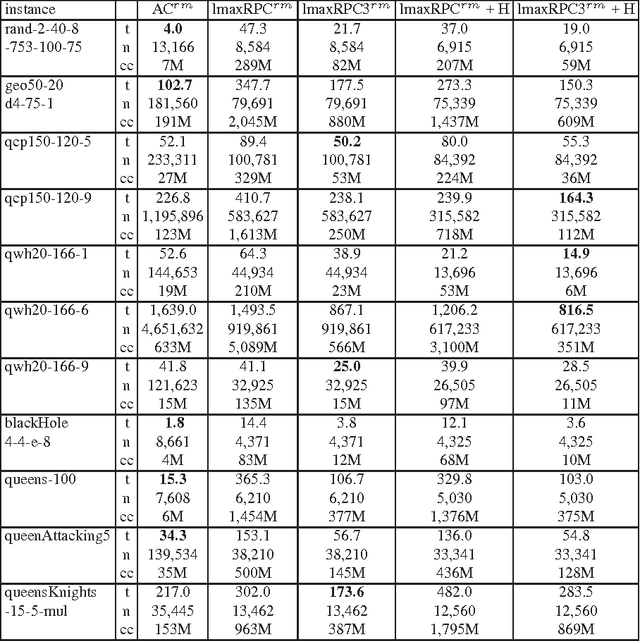
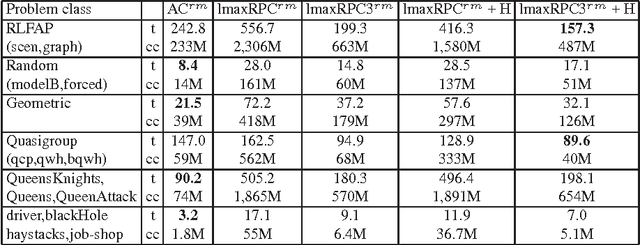
Max Restricted Path Consistency (maxRPC) is a local consistency for binary constraints that can achieve considerably stronger pruning than arc consistency. However, existing maxRRC algorithms suffer from overheads and redundancies as they can repeatedly perform many constraint checks without triggering any value deletions. In this paper we propose techniques that can boost the performance of maxRPC algorithms. These include the combined use of two data structures to avoid many redundant constraint checks, and heuristics for the efficient ordering and execution of certain operations. Based on these, we propose two closely related algorithms. The first one which is a maxRPC algorithm with optimal O(end^3) time complexity, displays good performance when used stand-alone, but is expensive to apply during search. The second one approximates maxRPC and has O(en^2d^4) time complexity, but a restricted version with O(end^4) complexity can be very efficient when used during search. Both algorithms have O(ed) space complexity. Experimental results demonstrate that the resulting methods constantly outperform previous algorithms for maxRPC, often by large margins, and constitute a more than viable alternative to arc consistency on many problems.

Evaluating and Improving Modern Variable and Revision Ordering Strategies in CSPs

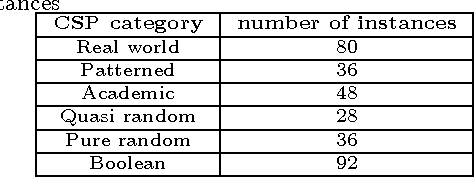
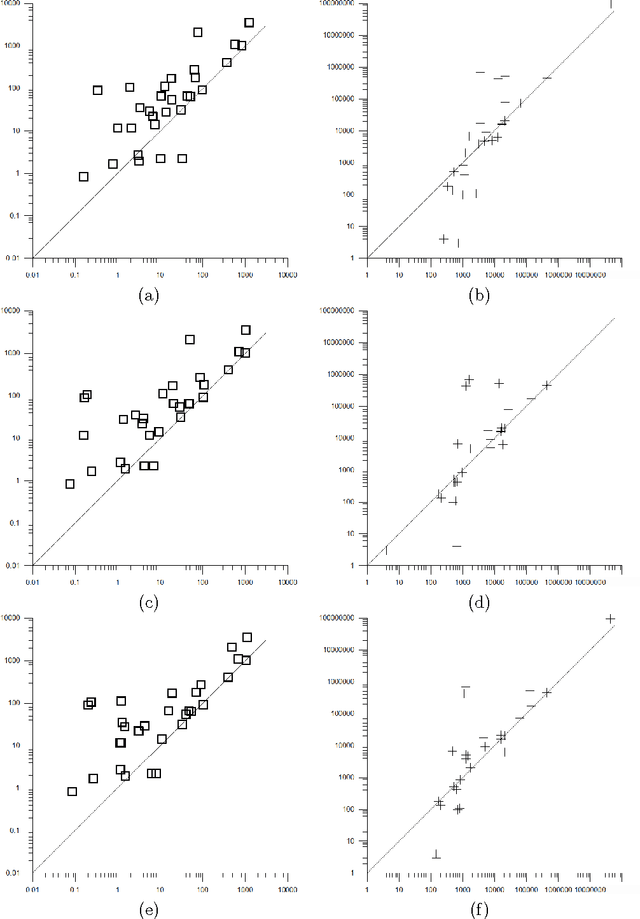
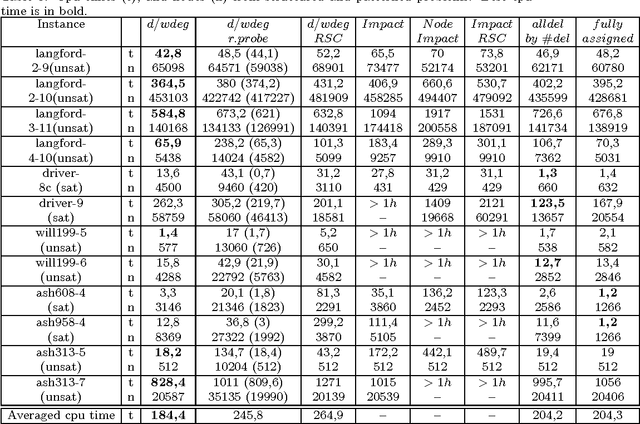
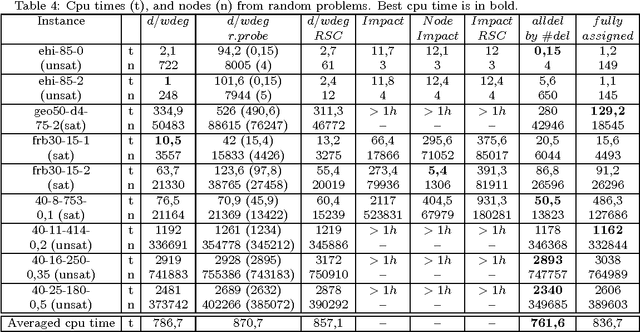
A key factor that can dramatically reduce the search space during constraint solving is the criterion under which the variable to be instantiated next is selected. For this purpose numerous heuristics have been proposed. Some of the best of such heuristics exploit information about failures gathered throughout search and recorded in the form of constraint weights, while others measure the importance of variable assignments in reducing the search space. In this work we experimentally evaluate the most recent and powerful variable ordering heuristics, and new variants of them, over a wide range of benchmarks. Results demonstrate that heuristics based on failures are in general more efficient. Based on this, we then derive new revision ordering heuristics that exploit recorded failures to efficiently order the propagation list when arc consistency is maintained during search. Interestingly, in addition to reducing the number of constraint checks and list operations, these heuristics are also able to cut down the size of the explored search tree.

Adaptive Branching for Constraint Satisfaction Problems

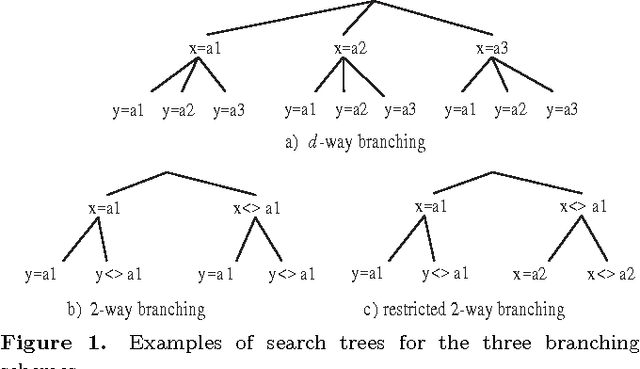
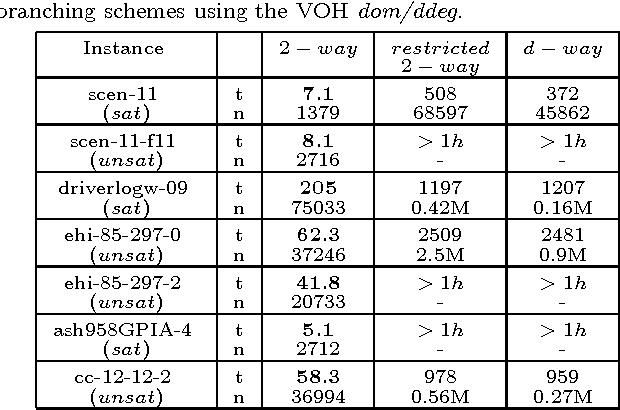
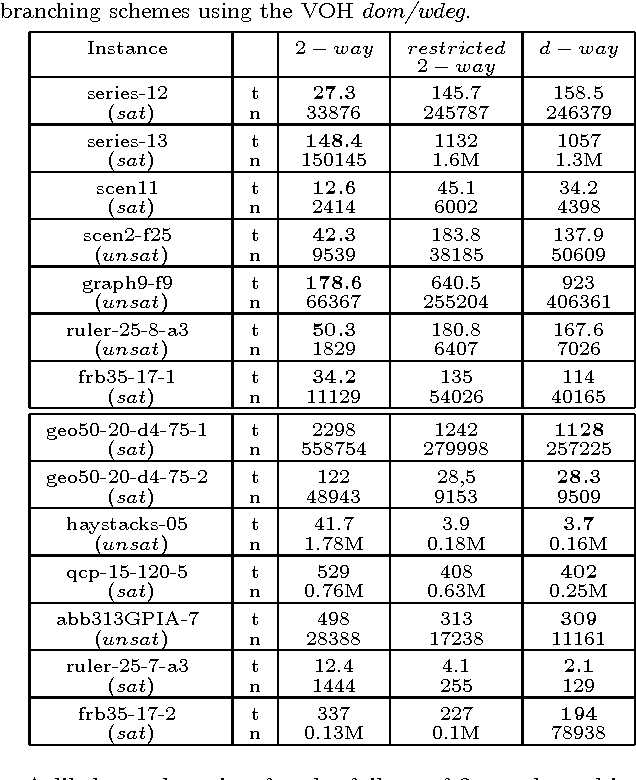
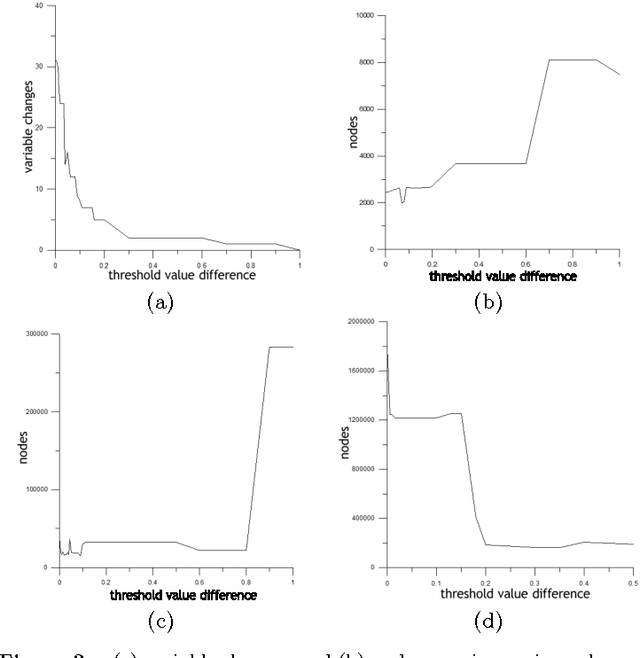
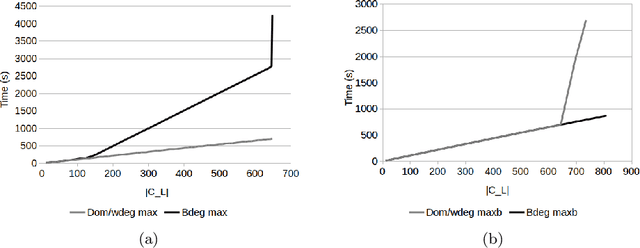
The two standard branching schemes for CSPs are d-way and 2-way branching. Although it has been shown that in theory the latter can be exponentially more effective than the former, there is a lack of empirical evidence showing such differences. To investigate this, we initially make an experimental comparison of the two branching schemes over a wide range of benchmarks. Experimental results verify the theoretical gap between d-way and 2-way branching as we move from a simple variable ordering heuristic like dom to more sophisticated ones like dom/ddeg. However, perhaps surprisingly, experiments also show that when state-of-the-art variable ordering heuristics like dom/wdeg are used then d-way can be clearly more efficient than 2-way branching in many cases. Motivated by this observation, we develop two generic heuristics that can be applied at certain points during search to decide whether 2-way branching or a restricted version of 2-way branching, which is close to d-way branching, will be followed. The application of these heuristics results in an adaptive branching scheme. Experiments with instantiations of the two generic heuristics confirm that search with adaptive branching outperforms search with a fixed branching scheme on a wide range of problems.