Experimental Evaluation of Branching Schemes for the CSP
Paper and Code
Sep 02, 2010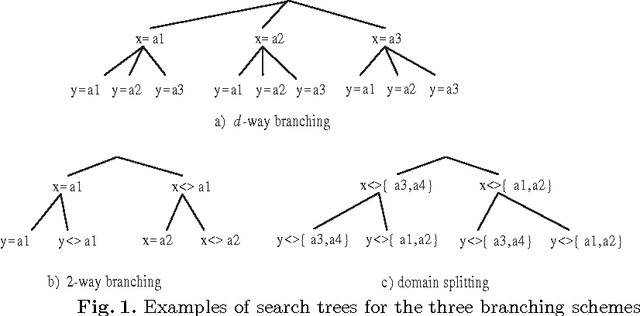
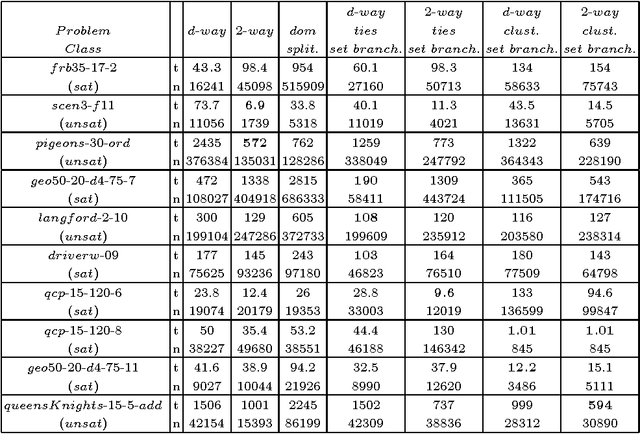
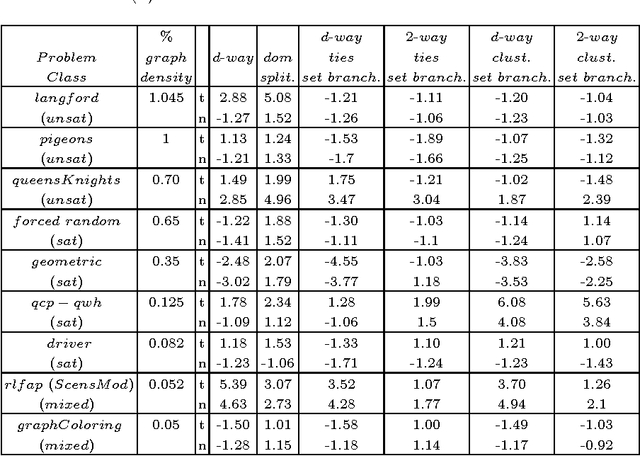
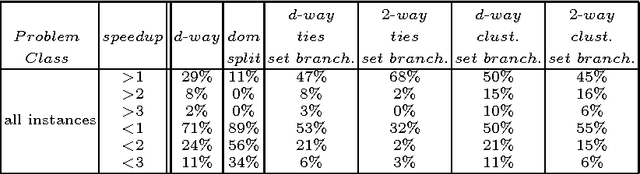
The search strategy of a CP solver is determined by the variable and value ordering heuristics it employs and by the branching scheme it follows. Although the effects of variable and value ordering heuristics on search effort have been widely studied, the effects of different branching schemes have received less attention. In this paper we study this effect through an experimental evaluation that includes standard branching schemes such as 2-way, d-way, and dichotomic domain splitting, as well as variations of set branching where branching is performed on sets of values. We also propose and evaluate a generic approach to set branching where the partition of a domain into sets is created using the scores assigned to values by a value ordering heuristic, and a clustering algorithm from machine learning. Experimental results demonstrate that although exponential differences between branching schemes, as predicted in theory between 2-way and d-way branching, are not very common, still the choice of branching scheme can make quite a difference on certain classes of problems. Set branching methods are very competitive with 2-way branching and outperform it on some problem classes. A statistical analysis of the results reveals that our generic clustering-based set branching method is the best among the methods compared.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge