Partial Queries for Constraint Acquisition

Learning constraint networks is known to require a number of membership queries exponential in the number of variables. In this paper, we learn constraint networks by asking the user partial queries. That is, we ask the user to classify assignments to subsets of the variables as positive or negative. We provide an algorithm, called QUACQ, that, given a negative example, focuses onto a constraint of the target network in a number of queries logarithmic in the size of the example. The whole constraint network can then be learned with a polynomial number of partial queries. We give information theoretic lower bounds for learning some simple classes of constraint networks and show that our generic algorithm is optimal in some cases.

Sketched Answer Set Programming

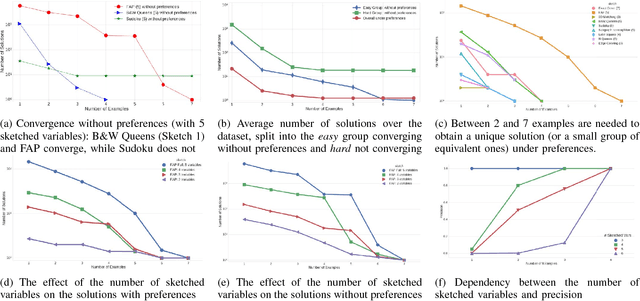
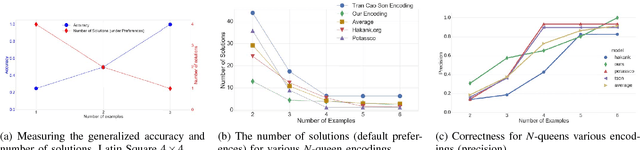
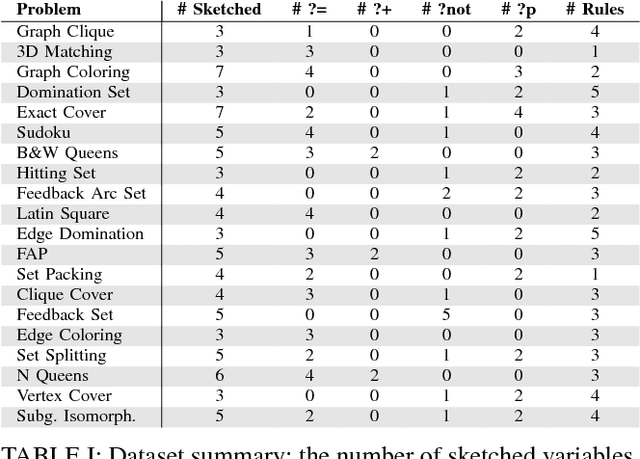
Answer Set Programming (ASP) is a powerful modeling formalism for combinatorial problems. However, writing ASP models is not trivial. We propose a novel method, called Sketched Answer Set Programming (SkASP), aiming at supporting the user in resolving this issue. The user writes an ASP program while marking uncertain parts open with question marks. In addition, the user provides a number of positive and negative examples of the desired program behaviour. The sketched model is rewritten into another ASP program, which is solved by traditional methods. As a result, the user obtains a functional and reusable ASP program modelling her problem. We evaluate our approach on 21 well known puzzles and combinatorial problems inspired by Karp's 21 NP-complete problems and demonstrate a use-case for a database application based on ASP.

Knowledge Compilation with Continuous Random Variables and its Application in Hybrid Probabilistic Logic Programming

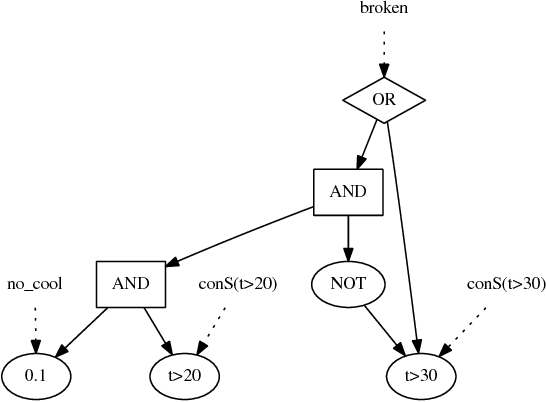
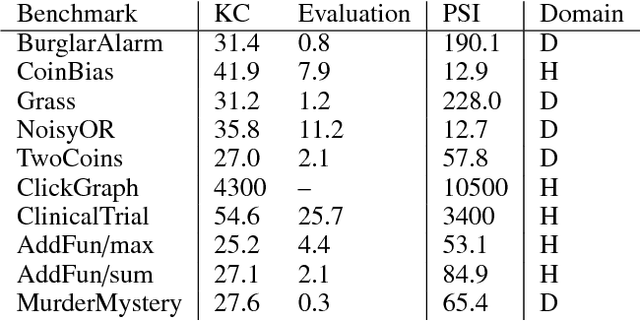
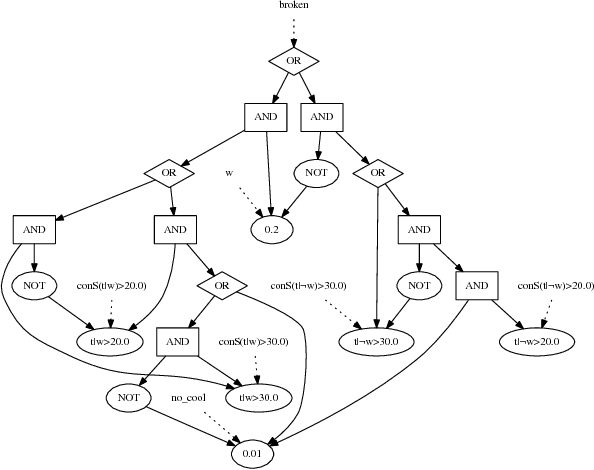
In probabilistic reasoning, the traditionally discrete domain has been elevated to the hybrid domain encompassing additionally continuous random variables. Inference in the hybrid domain, however, usually necessitates to condone trade-offs on either the inference on discrete or continuous random variables. We introduce a novel approach based on weighted model integration and algebraic model counting that circumvents these trade-offs. We then show how it supports knowledge compilation and exact probabilistic inference. Moreover, we introduce the hybrid probabilistic logic programming language HAL-ProbLog, an extension of ProbLog, to which we apply our inference approach.