Efficient semidefinite bounds for multi-label discrete graphical models

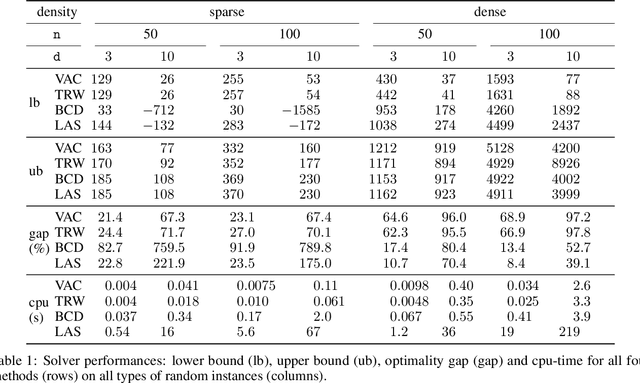
By concisely representing a joint function of many variables as the combination of small functions, discrete graphical models (GMs) provide a powerful framework to analyze stochastic and deterministic systems of interacting variables. One of the main queries on such models is to identify the extremum of this joint function. This is known as the Weighted Constraint Satisfaction Problem (WCSP) on deterministic Cost Function Networks and as Maximum a Posteriori (MAP) inference on stochastic Markov Random Fields. Algorithms for approximate WCSP inference typically rely on local consistency algorithms or belief propagation. These methods are intimately related to linear programming (LP) relaxations and often coupled with reparametrizations defined by the dual solution of the associated LP. Since the seminal work of Goemans and Williamson, it is well understood that convex SDP relaxations can provide superior guarantees to LP. But the inherent computational cost of interior point methods has limited their application. The situation has improved with the introduction of non-convex Burer-Monteiro style methods which are well suited to handle the SDP relaxation of combinatorial problems with binary variables (such as MAXCUT, MaxSAT or MAP/Ising). We compute low rank SDP upper and lower bounds for discrete pairwise graphical models with arbitrary number of values and arbitrary binary cost functions by extending a Burer-Monteiro style method based on row-by-row updates. We consider a traditional dualized constraint approach and a dedicated Block Coordinate Descent approach which avoids introducing large penalty coefficients to the formulation. On increasingly hard and dense WCSP/CFN instances, we observe that the BCD approach can outperform the dualized approach and provide tighter bounds than local consistencies/convergent message passing approaches.

Improved Acyclicity Reasoning for Bayesian Network Structure Learning with Constraint Programming

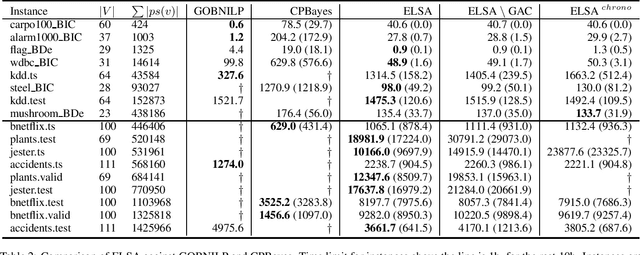
Bayesian networks are probabilistic graphical models with a wide range of application areas including gene regulatory networks inference, risk analysis and image processing. Learning the structure of a Bayesian network (BNSL) from discrete data is known to be an NP-hard task with a superexponential search space of directed acyclic graphs. In this work, we propose a new polynomial time algorithm for discovering a subset of all possible cluster cuts, a greedy algorithm for approximately solving the resulting linear program, and a generalised arc consistency algorithm for the acyclicity constraint. We embed these in the constraint programmingbased branch-and-bound solver CPBayes and show that, despite being suboptimal, they improve performance by orders of magnitude. The resulting solver also compares favourably with GOBNILP, a state-of-the-art solver for the BNSL problem which solves an NP-hard problem to discover each cut and solves the linear program exactly.

Partial Queries for Constraint Acquisition

Learning constraint networks is known to require a number of membership queries exponential in the number of variables. In this paper, we learn constraint networks by asking the user partial queries. That is, we ask the user to classify assignments to subsets of the variables as positive or negative. We provide an algorithm, called QUACQ, that, given a negative example, focuses onto a constraint of the target network in a number of queries logarithmic in the size of the example. The whole constraint network can then be learned with a polynomial number of partial queries. We give information theoretic lower bounds for learning some simple classes of constraint networks and show that our generic algorithm is optimal in some cases.

The Complexity of Integer Bound Propagation

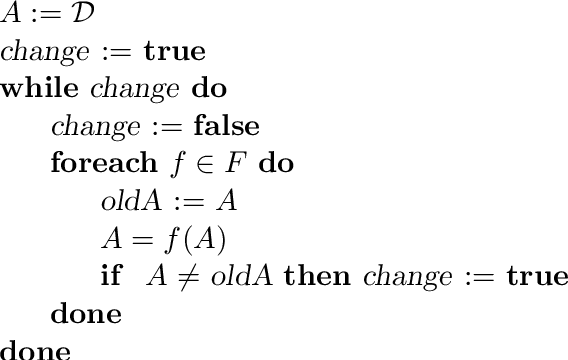
Bound propagation is an important Artificial Intelligence technique used in Constraint Programming tools to deal with numerical constraints. It is typically embedded within a search procedure ("branch and prune") and used at every node of the search tree to narrow down the search space, so it is critical that it be fast. The procedure invokes constraint propagators until a common fixpoint is reached, but the known algorithms for this have a pseudo-polynomial worst-case time complexity: they are fast indeed when the variables have a small numerical range, but they have the well-known problem of being prohibitively slow when these ranges are large. An important question is therefore whether strongly-polynomial algorithms exist that compute the common bound consistent fixpoint of a set of constraints. This paper answers this question. In particular we show that this fixpoint computation is in fact NP-complete, even when restricted to binary linear constraints.

The SeqBin Constraint Revisited

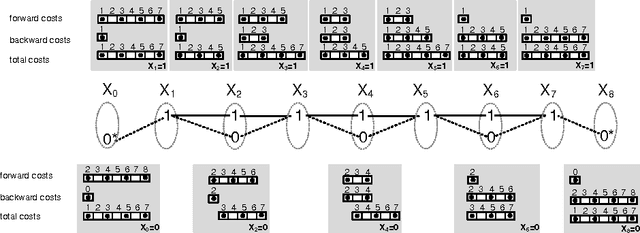
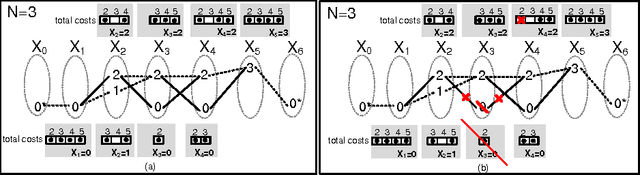
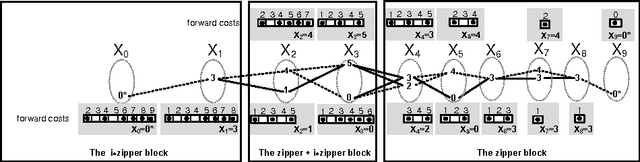
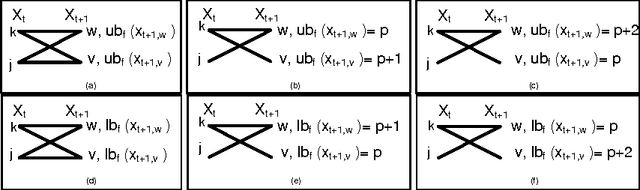
We revisit the SeqBin constraint. This meta-constraint subsumes a number of important global constraints like Change, Smooth and IncreasingNValue. We show that the previously proposed filtering algorithm for SeqBin has two drawbacks even under strong restrictions: it does not detect bounds disentailment and it is not idempotent. We identify the cause for these problems, and propose a new propagator that overcomes both issues. Our algorithm is based on a connection to the problem of finding a path of a given cost in a restricted $n$-partite graph. Our propagator enforces domain consistency in O(nd^2) and, for special cases of SeqBin that include Change, Smooth and IncreasingNValue, in O(nd) time.

Complexity of and Algorithms for Borda Manipulation

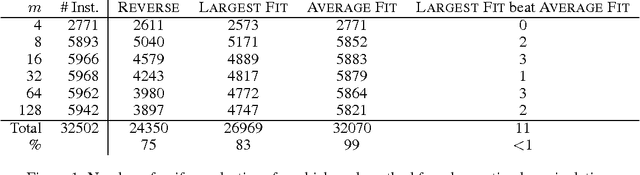
We prove that it is NP-hard for a coalition of two manipulators to compute how to manipulate the Borda voting rule. This resolves one of the last open problems in the computational complexity of manipulating common voting rules. Because of this NP-hardness, we treat computing a manipulation as an approximation problem where we try to minimize the number of manipulators. Based on ideas from bin packing and multiprocessor scheduling, we propose two new approximation methods to compute manipulations of the Borda rule. Experiments show that these methods significantly outperform the previous best known %existing approximation method. We are able to find optimal manipulations in almost all the randomly generated elections tested. Our results suggest that, whilst computing a manipulation of the Borda rule by a coalition is NP-hard, computational complexity may provide only a weak barrier against manipulation in practice.

An Empirical Study of Borda Manipulation

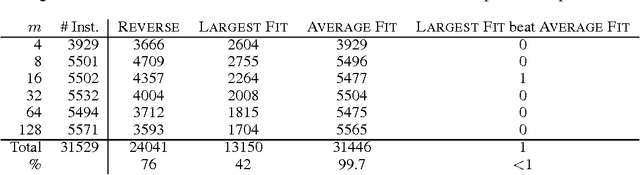
We study the problem of coalitional manipulation in elections using the unweighted Borda rule. We provide empirical evidence of the manipulability of Borda elections in the form of two new greedy manipulation algorithms based on intuitions from the bin-packing and multiprocessor scheduling domains. Although we have not been able to show that these algorithms beat existing methods in the worst-case, our empirical evaluation shows that they significantly outperform the existing method and are able to find optimal manipulations in the vast majority of the randomly generated elections that we tested. These empirical results provide further evidence that the Borda rule provides little defense against coalitional manipulation.

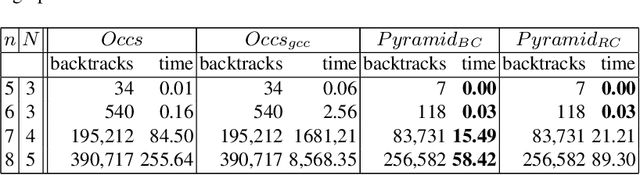
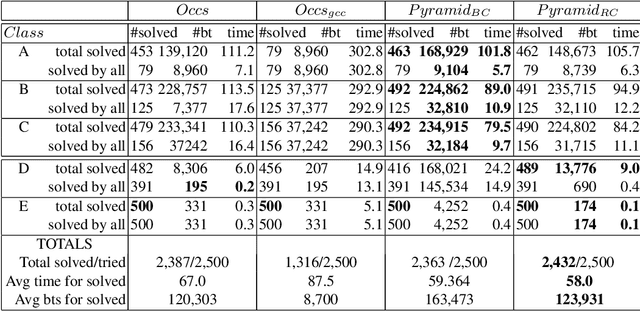
Decomposition of the NVALUE constraint

We study decompositions of the global NVALUE constraint. Our main contribution is theoretical: we show that there are propagators for global constraints like NVALUE which decomposition can simulate with the same time complexity but with a much greater space complexity. This suggests that the benefit of a global propagator may often not be in saving time but in saving space. Our other theoretical contribution is to show for the first time that range consistency can be enforced on NVALUE with the same worst-case time complexity as bound consistency. Finally, the decompositions we study are readily encoded as linear inequalities. We are therefore able to use them in integer linear programs.

On The Complexity and Completeness of Static Constraints for Breaking Row and Column Symmetry

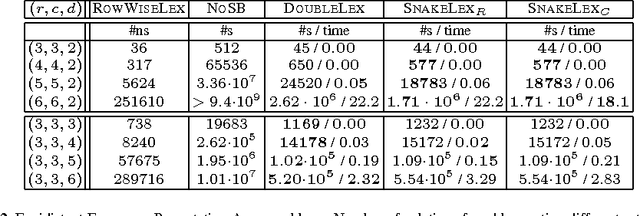
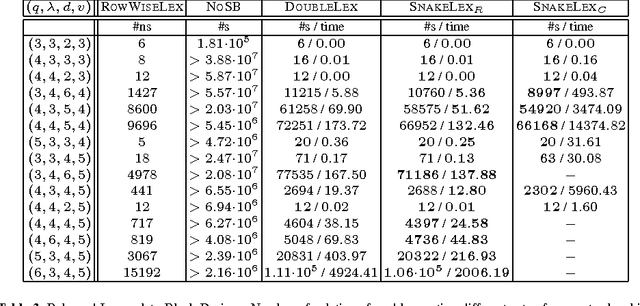
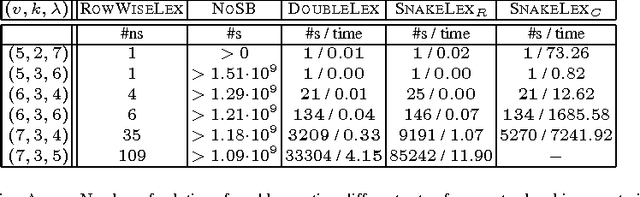
We consider a common type of symmetry where we have a matrix of decision variables with interchangeable rows and columns. A simple and efficient method to deal with such row and column symmetry is to post symmetry breaking constraints like DOUBLELEX and SNAKELEX. We provide a number of positive and negative results on posting such symmetry breaking constraints. On the positive side, we prove that we can compute in polynomial time a unique representative of an equivalence class in a matrix model with row and column symmetry if the number of rows (or of columns) is bounded and in a number of other special cases. On the negative side, we show that whilst DOUBLELEX and SNAKELEX are often effective in practice, they can leave a large number of symmetric solutions in the worst case. In addition, we prove that propagating DOUBLELEX completely is NP-hard. Finally we consider how to break row, column and value symmetry, correcting a result in the literature about the safeness of combining different symmetry breaking constraints. We end with the first experimental study on how much symmetry is left by DOUBLELEX and SNAKELEX on some benchmark problems.

Symmetries of Symmetry Breaking Constraints

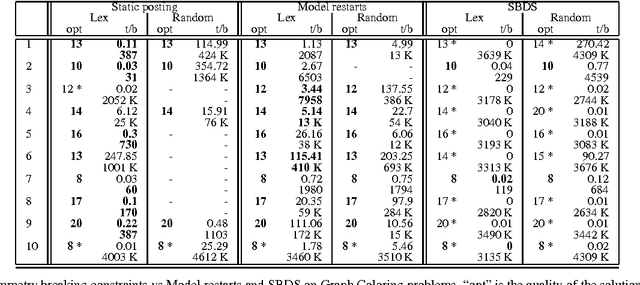
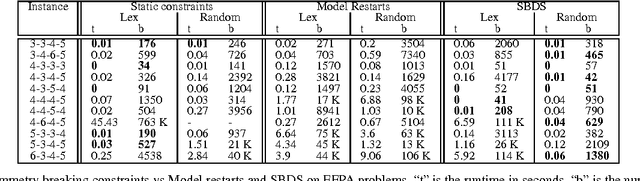
Symmetry is an important feature of many constraint programs. We show that any problem symmetry acting on a set of symmetry breaking constraints can be used to break symmetry. Different symmetries pick out different solutions in each symmetry class. This simple but powerful idea can be used in a number of different ways. We describe one application within model restarts, a search technique designed to reduce the conflict between symmetry breaking and the branching heuristic. In model restarts, we restart search periodically with a random symmetry of the symmetry breaking constraints. Experimental results show that this symmetry breaking technique is effective in practice on some standard benchmark problems.