A Symbolic SAT-based Algorithm for Almost-sure Reachability with Small Strategies in POMDPs

POMDPs are standard models for probabilistic planning problems, where an agent interacts with an uncertain environment. We study the problem of almost-sure reachability, where given a set of target states, the question is to decide whether there is a policy to ensure that the target set is reached with probability 1 (almost-surely). While in general the problem is EXPTIME-complete, in many practical cases policies with a small amount of memory suffice. Moreover, the existing solution to the problem is explicit, which first requires to construct explicitly an exponential reduction to a belief-support MDP. In this work, we first study the existence of observation-stationary strategies, which is NP-complete, and then small-memory strategies. We present a symbolic algorithm by an efficient encoding to SAT and using a SAT solver for the problem. We report experimental results demonstrating the scalability of our symbolic (SAT-based) approach.

Eliminating the Weakest Link: Making Manipulation Intractable?

Successive elimination of candidates is often a route to making manipulation intractable to compute. We prove that eliminating candidates does not necessarily increase the computational complexity of manipulation. However, for many voting rules used in practice, the computational complexity increases. For example, it is already known that it is NP-hard to compute how a single voter can manipulate the result of single transferable voting (the elimination version of plurality voting). We show here that it is NP-hard to compute how a single voter can manipulate the result of the elimination version of veto voting, of the closely related Coombs' rule, and of the elimination versions of a general class of scoring rules.

Complexity of and Algorithms for Borda Manipulation

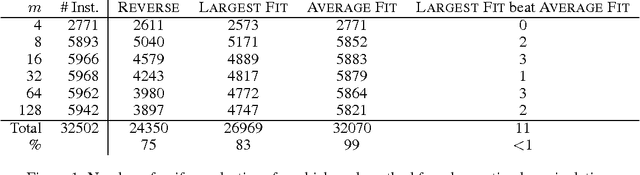
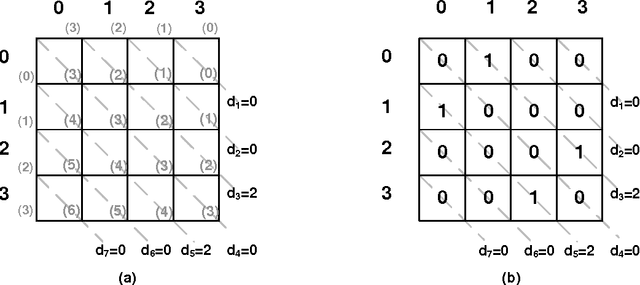
We prove that it is NP-hard for a coalition of two manipulators to compute how to manipulate the Borda voting rule. This resolves one of the last open problems in the computational complexity of manipulating common voting rules. Because of this NP-hardness, we treat computing a manipulation as an approximation problem where we try to minimize the number of manipulators. Based on ideas from bin packing and multiprocessor scheduling, we propose two new approximation methods to compute manipulations of the Borda rule. Experiments show that these methods significantly outperform the previous best known %existing approximation method. We are able to find optimal manipulations in almost all the randomly generated elections tested. Our results suggest that, whilst computing a manipulation of the Borda rule by a coalition is NP-hard, computational complexity may provide only a weak barrier against manipulation in practice.

An Empirical Study of Borda Manipulation

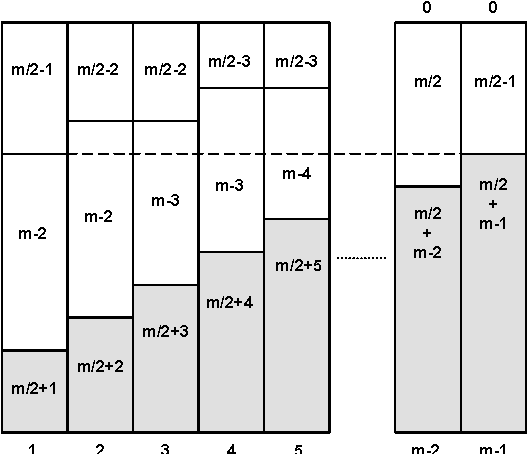
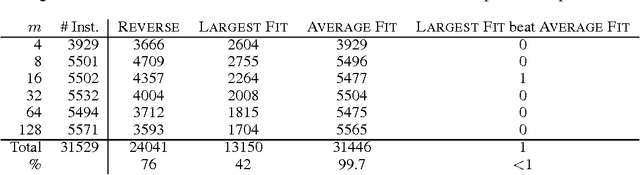
We study the problem of coalitional manipulation in elections using the unweighted Borda rule. We provide empirical evidence of the manipulability of Borda elections in the form of two new greedy manipulation algorithms based on intuitions from the bin-packing and multiprocessor scheduling domains. Although we have not been able to show that these algorithms beat existing methods in the worst-case, our empirical evaluation shows that they significantly outperform the existing method and are able to find optimal manipulations in the vast majority of the randomly generated elections that we tested. These empirical results provide further evidence that the Borda rule provides little defense against coalitional manipulation.