Scalable Coupling of Deep Learning with Logical Reasoning

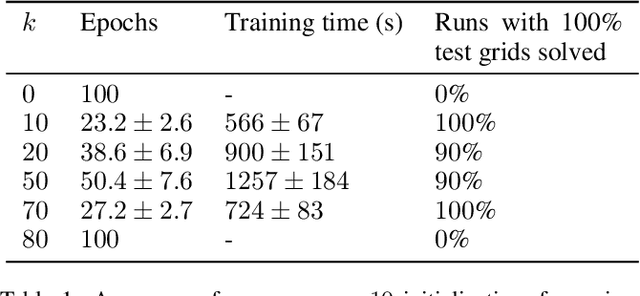
In the ongoing quest for hybridizing discrete reasoning with neural nets, there is an increasing interest in neural architectures that can learn how to solve discrete reasoning or optimization problems from natural inputs. In this paper, we introduce a scalable neural architecture and loss function dedicated to learning the constraints and criteria of NP-hard reasoning problems expressed as discrete Graphical Models. Our loss function solves one of the main limitations of Besag's pseudo-loglikelihood, enabling learning of high energies. We empirically show it is able to efficiently learn how to solve NP-hard reasoning problems from natural inputs as the symbolic, visual or many-solutions Sudoku problems as well as the energy optimization formulation of the protein design problem, providing data efficiency, interpretability, and \textit{a posteriori} control over predictions.

Efficient semidefinite bounds for multi-label discrete graphical models

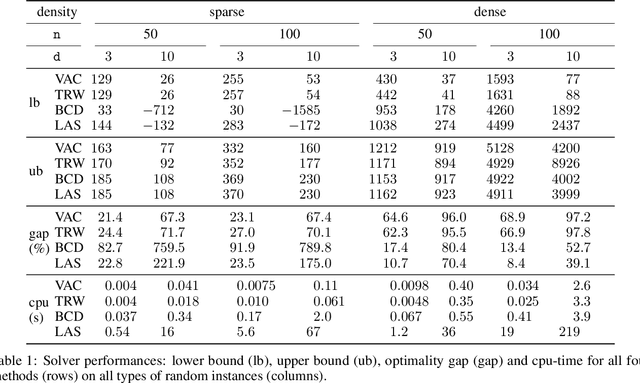
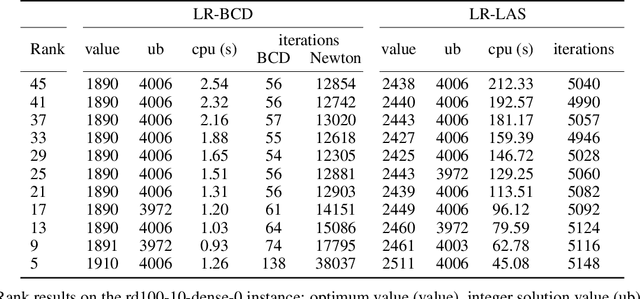
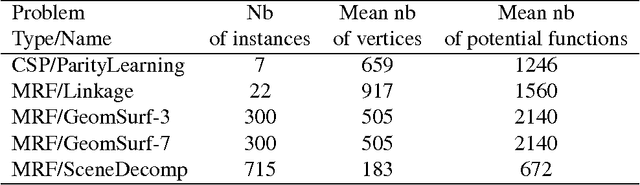
By concisely representing a joint function of many variables as the combination of small functions, discrete graphical models (GMs) provide a powerful framework to analyze stochastic and deterministic systems of interacting variables. One of the main queries on such models is to identify the extremum of this joint function. This is known as the Weighted Constraint Satisfaction Problem (WCSP) on deterministic Cost Function Networks and as Maximum a Posteriori (MAP) inference on stochastic Markov Random Fields. Algorithms for approximate WCSP inference typically rely on local consistency algorithms or belief propagation. These methods are intimately related to linear programming (LP) relaxations and often coupled with reparametrizations defined by the dual solution of the associated LP. Since the seminal work of Goemans and Williamson, it is well understood that convex SDP relaxations can provide superior guarantees to LP. But the inherent computational cost of interior point methods has limited their application. The situation has improved with the introduction of non-convex Burer-Monteiro style methods which are well suited to handle the SDP relaxation of combinatorial problems with binary variables (such as MAXCUT, MaxSAT or MAP/Ising). We compute low rank SDP upper and lower bounds for discrete pairwise graphical models with arbitrary number of values and arbitrary binary cost functions by extending a Burer-Monteiro style method based on row-by-row updates. We consider a traditional dualized constraint approach and a dedicated Block Coordinate Descent approach which avoids introducing large penalty coefficients to the formulation. On increasingly hard and dense WCSP/CFN instances, we observe that the BCD approach can outperform the dualized approach and provide tighter bounds than local consistencies/convergent message passing approaches.

Exact and approximate inference in graphical models: variable elimination and beyond

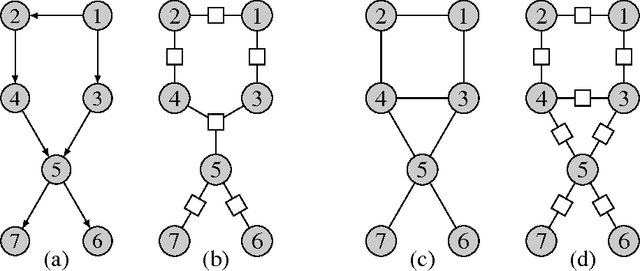
Probabilistic graphical models offer a powerful framework to account for the dependence structure between variables, which is represented as a graph. However, the dependence between variables may render inference tasks intractable. In this paper we review techniques exploiting the graph structure for exact inference, borrowed from optimisation and computer science. They are built on the principle of variable elimination whose complexity is dictated in an intricate way by the order in which variables are eliminated. The so-called treewidth of the graph characterises this algorithmic complexity: low-treewidth graphs can be processed efficiently. The first message that we illustrate is therefore the idea that for inference in graphical model, the number of variables is not the limiting factor, and it is worth checking for the treewidth before turning to approximate methods. We show how algorithms providing an upper bound of the treewidth can be exploited to derive a 'good' elimination order enabling to perform exact inference. The second message is that when the treewidth is too large, algorithms for approximate inference linked to the principle of variable elimination, such as loopy belief propagation and variational approaches, can lead to accurate results while being much less time consuming than Monte-Carlo approaches. We illustrate the techniques reviewed in this article on benchmarks of inference problems in genetic linkage analysis and computer vision, as well as on hidden variables restoration in coupled Hidden Markov Models.

Tractability and Decompositions of Global Cost Functions

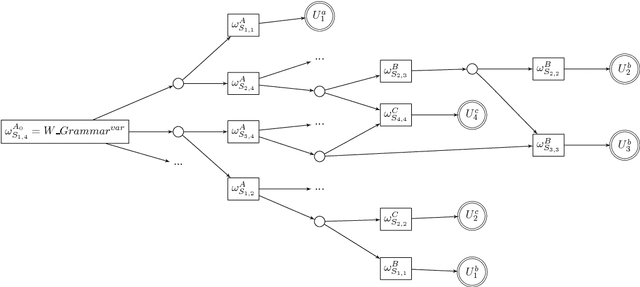
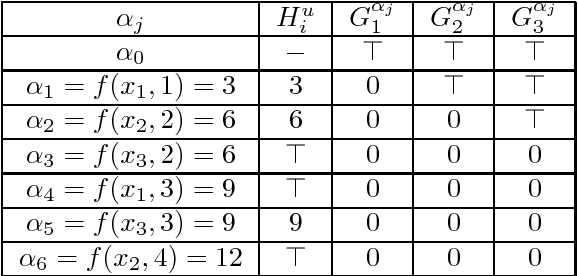
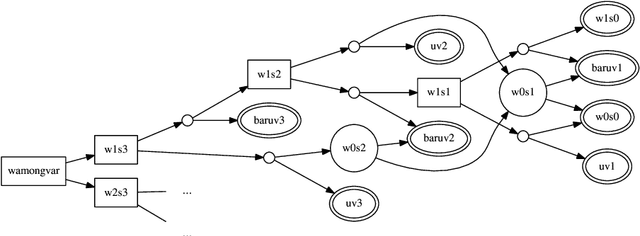
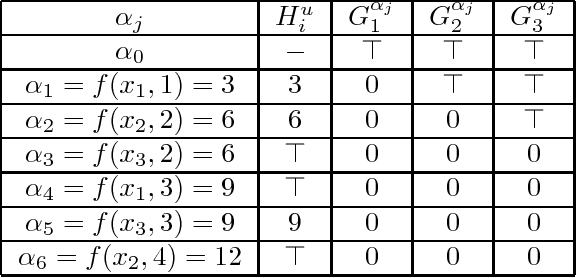
Enforcing local consistencies in cost function networks is performed by applying so-called Equivalent Preserving Transformations (EPTs) to the cost functions. As EPTs transform the cost functions, they may break the property that was making local consistency enforcement tractable on a global cost function. A global cost function is called tractable projection-safe when applying an EPT to it is tractable and does not break the tractability property. In this paper, we prove that depending on the size r of the smallest scopes used for performing EPTs, the tractability of global cost functions can be preserved (r = 0) or destroyed (r > 1). When r = 1, the answer is indefinite. We show that on a large family of cost functions, EPTs can be computed via dynamic programming-based algorithms, leading to tractable projection-safety. We also show that when a global cost function can be decomposed into a Berge acyclic network of bounded arity cost functions, soft local consistencies such as soft Directed or Virtual Arc Consistency can directly emulate dynamic programming. These different approaches to decomposable cost functions are then embedded in a solver for extensive experiments that confirm the feasibility and efficiency of our proposal.

Bounds Arc Consistency for Weighted CSPs

The Weighted Constraint Satisfaction Problem (WCSP) framework allows representing and solving problems involving both hard constraints and cost functions. It has been applied to various problems, including resource allocation, bioinformatics, scheduling, etc. To solve such problems, solvers usually rely on branch-and-bound algorithms equipped with local consistency filtering, mostly soft arc consistency. However, these techniques are not well suited to solve problems with very large domains. Motivated by the resolution of an RNA gene localization problem inside large genomic sequences, and in the spirit of bounds consistency for large domains in crisp CSPs, we introduce soft bounds arc consistency, a new weighted local consistency specifically designed for WCSP with very large domains. Compared to soft arc consistency, BAC provides significantly improved time and space asymptotic complexity. In this paper, we show how the semantics of cost functions can be exploited to further improve the time complexity of BAC. We also compare both in theory and in practice the efficiency of BAC on a WCSP with bounds consistency enforced on a crisp CSP using cost variables. On two different real problems modeled as WCSP, including our RNA gene localization problem, we observe that maintaining bounds arc consistency outperforms arc consistency and also improves over bounds consistency enforced on a constraint model with cost variables.

Possibilistic Constraint Satisfaction Problems or "How to handle soft constraints?"

Many AI synthesis problems such as planning or scheduling may be modelized as constraint satisfaction problems (CSP). A CSP is typically defined as the problem of finding any consistent labeling for a fixed set of variables satisfying all given constraints between these variables. However, for many real tasks such as job-shop scheduling, time-table scheduling, design?, all these constraints have not the same significance and have not to be necessarily satisfied. A first distinction can be made between hard constraints, which every solution should satisfy and soft constraints, whose satisfaction has not to be certain. In this paper, we formalize the notion of possibilistic constraint satisfaction problems that allows the modeling of uncertainly satisfied constraints. We use a possibility distribution over labelings to represent respective possibilities of each labeling. Necessity-valued constraints allow a simple expression of the respective certainty degrees of each constraint. The main advantage of our approach is its integration in the CSP technical framework. Most classical techniques, such as Backtracking (BT), arcconsistency enforcing (AC) or Forward Checking have been extended to handle possibilistics CSP and are effectively implemented. The utility of our approach is demonstrated on a simple design problem.

Penalty logic and its Link with Dempster-Shafer Theory

Penalty logic, introduced by Pinkas, associates to each formula of a knowledge base the price to pay if this formula is violated. Penalties may be used as a criterion for selecting preferred consistent subsets in an inconsistent knowledge base, thus inducing a non-monotonic inference relation. A precise formalization and the main properties of penalty logic and of its associated non-monotonic inference relation are given in the first part. We also show that penalty logic and Dempster-Shafer theory are related, especially in the infinitesimal case.

A Constraint Satisfaction Approach to Decision under Uncertainty

The Constraint Satisfaction Problem (CSP) framework offers a simple and sound basis for representing and solving simple decision problems, without uncertainty. This paper is devoted to an extension of the CSP framework enabling us to deal with some decisions problems under uncertainty. This extension relies on a differentiation between the agent-controllable decision variables and the uncontrollable parameters whose values depend on the occurrence of uncertain events. The uncertainty on the values of the parameters is assumed to be given under the form of a probability distribution. Two algorithms are given, for computing respectively decisions solving the problem with a maximal probability, and conditional decisions mapping the largest possible amount of possible cases to actual decisions.

From influence diagrams to multi-operator cluster DAGs

There exist several architectures to solve influence diagrams using local computations, such as the Shenoy-Shafer, the HUGIN, or the Lazy Propagation architectures. They all extend usual variable elimination algorithms thanks to the use of so-called 'potentials'. In this paper, we introduce a new architecture, called the Multi-operator Cluster DAG architecture, which can produce decompositions with an improved constrained induced-width, and therefore induce potentially exponential gains. Its principle is to benefit from the composite nature of influence diagrams, instead of using uniform potentials, in order to better analyze the problem structure.

Arc consistency for soft constraints

The notion of arc consistency plays a central role in constraint satisfaction. It is known that the notion of local consistency can be extended to constraint optimisation problems defined by soft constraint frameworks based on an idempotent cost combination operator. This excludes non idempotent operators such as + which define problems which are very important in practical applications such as Max-CSP, where the aim is to minimize the number of violated constraints. In this paper, we show that using a weak additional axiom satisfied by most existing soft constraints proposals, it is possible to define a notion of soft arc consistency that extends the classical notion of arc consistency and this even in the case of non idempotent cost combination operators. A polynomial time algorithm for enforcing this soft arc consistency exists and its space and time complexities are identical to that of enforcing arc consistency in CSPs when the cost combination operator is strictly monotonic (for example Max-CSP). A directional version of arc consistency is potentially even stronger than the non-directional version, since it allows non local propagation of penalties. We demonstrate the utility of directional arc consistency by showing that it not only solves soft constraint problems on trees, but that it also implies a form of local optimality, which we call arc irreducibility.