Probabilistic Conditional Preference Networks

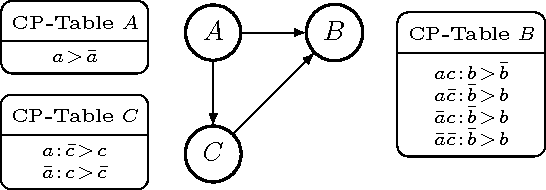
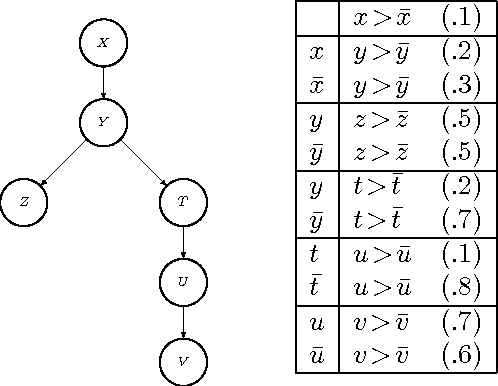
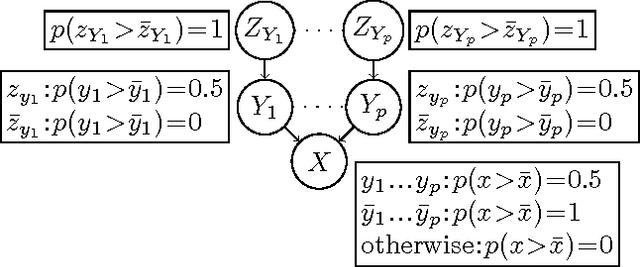
In order to represent the preferences of a group of individuals, we introduce Probabilistic CP-nets (PCP-nets). PCP-nets provide a compact language for representing probability distributions over preference orderings. We argue that they are useful for aggregating preferences or modelling noisy preferences. Then we give efficient algorithms for the main reasoning problems, namely for computing the probability that a given outcome is preferred to another one, and the probability that a given outcome is optimal. As a by-product, we obtain an unexpected linear-time algorithm for checking dominance in a standard, tree-structured CP-net.

A Constraint Satisfaction Approach to Decision under Uncertainty

The Constraint Satisfaction Problem (CSP) framework offers a simple and sound basis for representing and solving simple decision problems, without uncertainty. This paper is devoted to an extension of the CSP framework enabling us to deal with some decisions problems under uncertainty. This extension relies on a differentiation between the agent-controllable decision variables and the uncontrollable parameters whose values depend on the occurrence of uncertain events. The uncertainty on the values of the parameters is assumed to be given under the form of a probability distribution. Two algorithms are given, for computing respectively decisions solving the problem with a maximal probability, and conditional decisions mapping the largest possible amount of possible cases to actual decisions.

Decision-making Under Ordinal Preferences and Comparative Uncertainty

This paper investigates the problem of finding a preference relation on a set of acts from the knowledge of an ordering on events (subsets of states of the world) describing the decision-maker (DM)s uncertainty and an ordering of consequences of acts, describing the DMs preferences. However, contrary to classical approaches to decision theory, we try to do it without resorting to any numerical representation of utility nor uncertainty, and without even using any qualitative scale on which both uncertainty and preference could be mapped. It is shown that although many axioms of Savage theory can be preserved and despite the intuitive appeal of the method for constructing a preference over acts, the approach is inconsistent with a probabilistic representation of uncertainty, but leads to the kind of uncertainty theory encountered in non-monotonic reasoning (especially preferential and rational inference), closely related to possibility theory. Moreover the method turns out to be either very little decisive or to lead to very risky decisions, although its basic principles look sound. This paper raises the question of the very possibility of purely symbolic approaches to Savage-like decision-making under uncertainty and obtains preliminary negative results.

Comparative Uncertainty, Belief Functions and Accepted Beliefs

This paper relates comparative belief structures and a general view of belief management in the setting of deductively closed logical representations of accepted beliefs. We show that the range of compatibility between the classical deductive closure and uncertain reasoning covers precisely the nonmonotonic 'preferential' inference system of Kraus, Lehmann and Magidor and nothing else. In terms of uncertain reasoning any possibility or necessity measure gives birth to a structure of accepted beliefs. The classes of probability functions and of Shafer's belief functions which yield belief sets prove to be very special ones.

Qualitative Models for Decision Under Uncertainty without the Commensurability Assumption

This paper investigates a purely qualitative version of Savage's theory for decision making under uncertainty. Until now, most representation theorems for preference over acts rely on a numerical representation of utility and uncertainty where utility and uncertainty are commensurate. Disrupting the tradition, we relax this assumption and introduce a purely ordinal axiom requiring that the Decision Maker (DM) preference between two acts only depends on the relative position of their consequences for each state. Within this qualitative framework, we determine the only possible form of the decision rule and investigate some instances compatible with the transitivity of the strict preference. Finally we propose a mild relaxation of our ordinality axiom, leaving room for a new family of qualitative decision rules compatible with transitivity.

A Unified framework for order-of-magnitude confidence relations

The aim of this work is to provide a unified framework for ordinal representations of uncertainty lying at the crosswords between possibility and probability theories. Such confidence relations between events are commonly found in monotonic reasoning, inconsistency management, or qualitative decision theory. They start either from probability theory, making it more qualitative, or from possibility theory, making it more expressive. We show these two trends converge to a class of genuine probability theories. We provide characterization results for these useful tools that preserve the qualitative nature of possibility rankings, while enjoying the power of expressivity of additive representations.

On the Complexity of Decision Making in Possibilistic Decision Trees

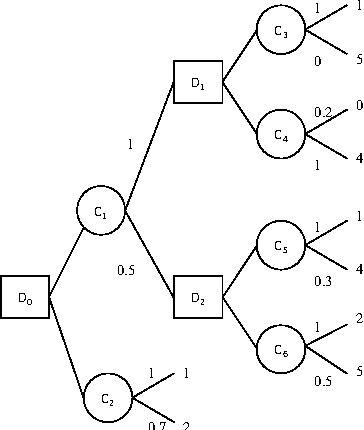
When the information about uncertainty cannot be quantified in a simple, probabilistic way, the topic of possibilistic decision theory is often a natural one to consider. The development of possibilistic decision theory has lead to a series of possibilistic criteria, e.g pessimistic possibilistic qualitative utility, possibilistic likely dominance, binary possibilistic utility and possibilistic Choquet integrals. This paper focuses on sequential decision making in possibilistic decision trees. It proposes a complexity study of the problem of finding an optimal strategy depending on the monotonicity property of the optimization criteria which allows the application of dynamic programming that offers a polytime reduction of the decision problem. It also shows that possibilistic Choquet integrals do not satisfy this property, and that in this case the optimization problem is NP - hard.