An elementary belief function logic

Non-additive uncertainty theories, typically possibility theory, belief functions and imprecise probabilities share a common feature with modal logic: the duality properties between possibility and necessity measures, belief and plausibility functions as well as between upper and lower probabilities extend the duality between possibility and necessity modalities to the graded environment. It has been shown that the all-or-nothing version of possibility theory can be exactly captured by a minimal epistemic logic (MEL) that uses a very small fragment of the KD modal logic, without resorting to relational semantics. Besides, the case of belief functions has been studied independently, and a belief function logic has been obtained by extending the modal logic S5 to graded modalities using {\L}ukasiewicz logic, albeit using relational semantics. This paper shows that a simpler belief function logic can be devised by adding {\L}ukasiewicz logic on top of MEL. It allows for a more natural semantics in terms of Shafer basic probability assignments.

From Shallow to Deep Interactions Between Knowledge Representation, Reasoning and Machine Learning (Kay R. Amel group)

This paper proposes a tentative and original survey of meeting points between Knowledge Representation and Reasoning (KRR) and Machine Learning (ML), two areas which have been developing quite separately in the last three decades. Some common concerns are identified and discussed such as the types of used representation, the roles of knowledge and data, the lack or the excess of information, or the need for explanations and causal understanding. Then some methodologies combining reasoning and learning are reviewed (such as inductive logic programming, neuro-symbolic reasoning, formal concept analysis, rule-based representations and ML, uncertainty in ML, or case-based reasoning and analogical reasoning), before discussing examples of synergies between KRR and ML (including topics such as belief functions on regression, EM algorithm versus revision, the semantic description of vector representations, the combination of deep learning with high level inference, knowledge graph completion, declarative frameworks for data mining, or preferences and recommendation). This paper is the first step of a work in progress aiming at a better mutual understanding of research in KRR and ML, and how they could cooperate.

On the Qualitative Comparison of Decisions Having Positive and Negative Features

Making a decision is often a matter of listing and comparing positive and negative arguments. In such cases, the evaluation scale for decisions should be considered bipolar, that is, negative and positive values should be explicitly distinguished. That is what is done, for example, in Cumulative Prospect Theory. However, contraryto the latter framework that presupposes genuine numerical assessments, human agents often decide on the basis of an ordinal ranking of the pros and the cons, and by focusing on the most salient arguments. In other terms, the decision process is qualitative as well as bipolar. In this article, based on a bipolar extension of possibility theory, we define and axiomatically characterize several decision rules tailored for the joint handling of positive and negative arguments in an ordinal setting. The simplest rules can be viewed as extensions of the maximin and maximax criteria to the bipolar case, and consequently suffer from poor decisive power. More decisive rules that refine the former are also proposed. These refinements agree both with principles of efficiency and with the spirit of order-of-magnitude reasoning, that prevails in qualitative decision theory. The most refined decision rule uses leximin rankings of the pros and the cons, and the ideas of counting arguments of equal strength and cancelling pros by cons. It is shown to come down to a special case of Cumulative Prospect Theory, and to subsume the Take the Best heuristic studied by cognitive psychologists.

Qualitative Possibilistic Mixed-Observable MDPs

Possibilistic and qualitative POMDPs (pi-POMDPs) are counterparts of POMDPs used to model situations where the agent's initial belief or observation probabilities are imprecise due to lack of past experiences or insufficient data collection. However, like probabilistic POMDPs, optimally solving pi-POMDPs is intractable: the finite belief state space exponentially grows with the number of system's states. In this paper, a possibilistic version of Mixed-Observable MDPs is presented to get around this issue: the complexity of solving pi-POMDPs, some state variables of which are fully observable, can be then dramatically reduced. A value iteration algorithm for this new formulation under infinite horizon is next proposed and the optimality of the returned policy (for a specified criterion) is shown assuming the existence of a "stay" action in some goal states. Experimental work finally shows that this possibilistic model outperforms probabilistic POMDPs commonly used in robotics, for a target recognition problem where the agent's observations are imprecise.

Proceedings of the Eighth Conference on Uncertainty in Artificial Intelligence (1992)

This is the Proceedings of the Eighth Conference on Uncertainty in Artificial Intelligence, which was held in Stanford, CA, July 17-19, 1992

Modeling uncertain and vague knowledge in possibility and evidence theories

This paper advocates the usefulness of new theories of uncertainty for the purpose of modeling some facets of uncertain knowledge, especially vagueness, in AI. It can be viewed as a partial reply to Cheeseman's (among others) defense of probability.

Automated Reasoning Using Possibilistic Logic: Semantics, Belief Revision and Variable Certainty Weights

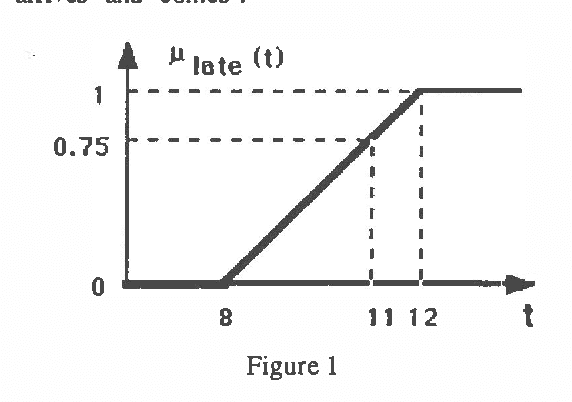
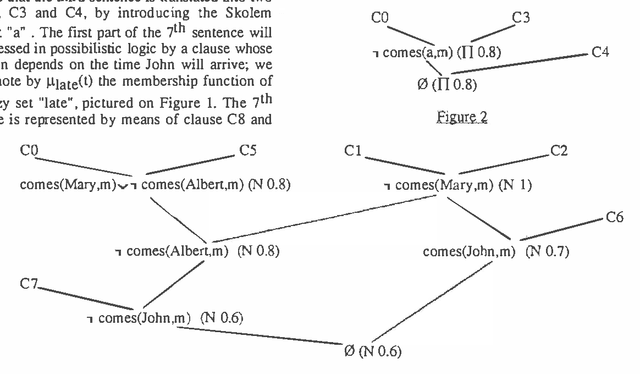
In this paper an approach to automated deduction under uncertainty,based on possibilistic logic, is proposed ; for that purpose we deal with clauses weighted by a degree which is a lower bound of a necessity or a possibility measure, according to the nature of the uncertainty. Two resolution rules are used for coping with the different situations, and the refutation method can be generalized. Besides the lower bounds are allowed to be functions of variables involved in the clause, which gives hypothetical reasoning capabilities. The relation between our approach and the idea of minimizing abnormality is briefly discussed. In case where only lower bounds of necessity measures are involved, a semantics is proposed, in which the completeness of the extended resolution principle is proved. Moreover deduction from a partially inconsistent knowledge base can be managed in this approach and displays some form of non-monotonicity.

Updating with Belief Functions, Ordinal Conditioning Functions and Possibility Measures

This paper discusses how a measure of uncertainty representing a state of knowledge can be updated when a new information, which may be pervaded with uncertainty, becomes available. This problem is considered in various framework, namely: Shafer's evidence theory, Zadeh's possibility theory, Spohn's theory of epistemic states. In the two first cases, analogues of Jeffrey's rule of conditioning are introduced and discussed. The relations between Spohn's model and possibility theory are emphasized and Spohn's updating rule is contrasted with the Jeffrey-like rule of conditioning in possibility theory. Recent results by Shenoy on the combination of ordinal conditional functions are reinterpreted in the language of possibility theory. It is shown that Shenoy's combination rule has a well-known possibilistic counterpart.

A Logic of Graded Possibility and Certainty Coping with Partial Inconsistency

A semantics is given to possibilistic logic, a logic that handles weighted classical logic formulae, and where weights are interpreted as lower bounds on degrees of certainty or possibility, in the sense of Zadeh's possibility theory. The proposed semantics is based on fuzzy sets of interpretations. It is tolerant to partial inconsistency. Satisfiability is extended from interpretations to fuzzy sets of interpretations, each fuzzy set representing a possibility distribution describing what is known about the state of the world. A possibilistic knowledge base is then viewed as a set of possibility distributions that satisfy it. The refutation method of automated deduction in possibilistic logic, based on previously introduced generalized resolution principle is proved to be sound and complete with respect to the proposed semantics, including the case of partial inconsistency.

Constraint Propagation with Imprecise Conditional Probabilities

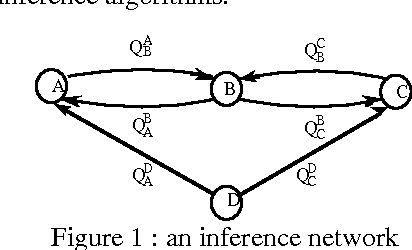
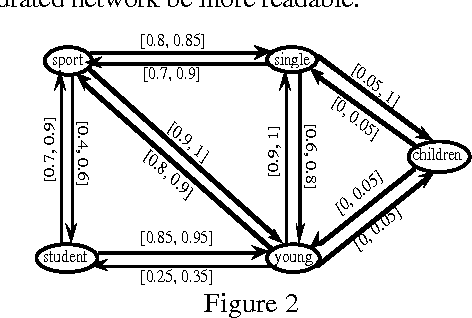
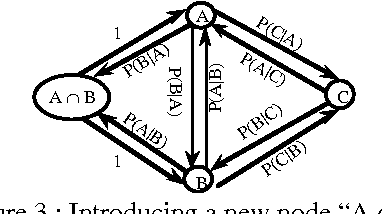
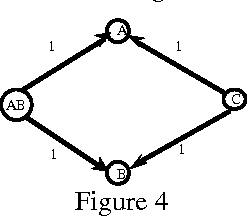
An approach to reasoning with default rules where the proportion of exceptions, or more generally the probability of encountering an exception, can be at least roughly assessed is presented. It is based on local uncertainty propagation rules which provide the best bracketing of a conditional probability of interest from the knowledge of the bracketing of some other conditional probabilities. A procedure that uses two such propagation rules repeatedly is proposed in order to estimate any simple conditional probability of interest from the available knowledge. The iterative procedure, that does not require independence assumptions, looks promising with respect to the linear programming method. Improved bounds for conditional probabilities are given when independence assumptions hold.