Rotations of Gödel algebras with modal operators

The present paper is devoted to study the effect of connected and disconnected rotations of G\"odel algebras with operators grounded on directly indecomposable structures. The structures resulting from this construction we will present are nilpotent minimum (with or without negation fixpoint, depending on whether the rotation is connected or disconnected) with special modal operators defined on a directly indecomposable algebra. In this paper we will present a (quasi-)equational definition of these latter structures. Our main results show that directly indecomposable nilpotent minimum algebras (with or without negation fixpoint) with modal operators are fully characterized as connected and disconnected rotations of directly indecomposable G\"odel algebras endowed with modal operators.

An elementary belief function logic

Non-additive uncertainty theories, typically possibility theory, belief functions and imprecise probabilities share a common feature with modal logic: the duality properties between possibility and necessity measures, belief and plausibility functions as well as between upper and lower probabilities extend the duality between possibility and necessity modalities to the graded environment. It has been shown that the all-or-nothing version of possibility theory can be exactly captured by a minimal epistemic logic (MEL) that uses a very small fragment of the KD modal logic, without resorting to relational semantics. Besides, the case of belief functions has been studied independently, and a belief function logic has been obtained by extending the modal logic S5 to graded modalities using {\L}ukasiewicz logic, albeit using relational semantics. This paper shows that a simpler belief function logic can be devised by adding {\L}ukasiewicz logic on top of MEL. It allows for a more natural semantics in terms of Shafer basic probability assignments.

Simplified Kripke semantics for K45-like Godel modal logics and its axiomatic extensions

In this paper, we provide simplified semantics for the logic K45(G), i.e. the many-valued Godel counterpart of the classical modal logic K45. More precisely, we characterize K45(G) as the set of valid formulae of the class of possibilistic Godel Kripke Frames <W,\pi> where W is a non-empty set of worlds and \pi: W \to [0, 1] is a possibility distribution on W.

Combining Multiple-Valued Logics in Modular Expert Systems

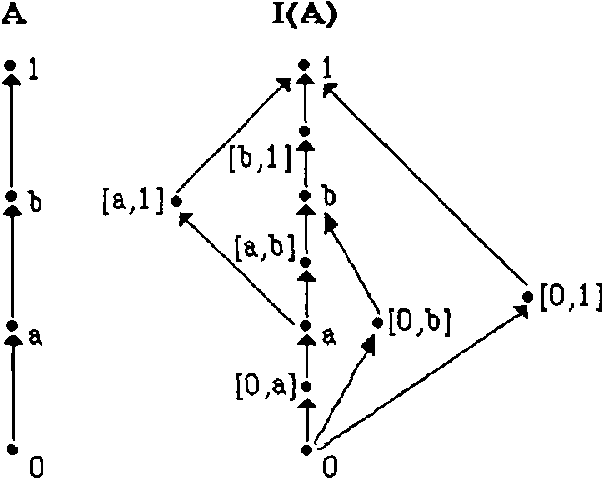
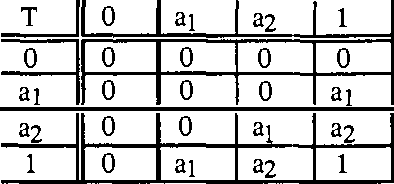
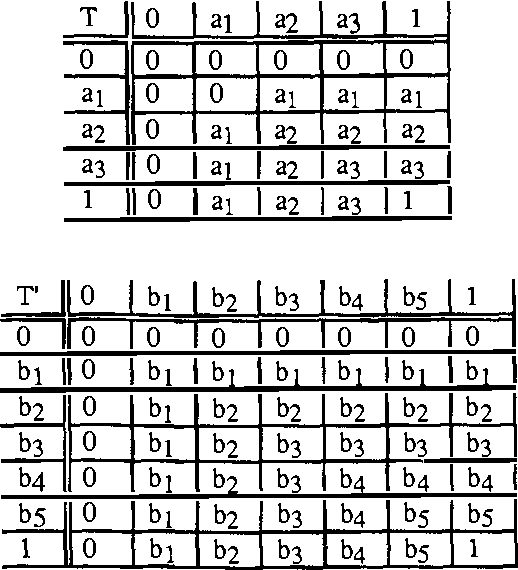
The way experts manage uncertainty usually changes depending on the task they are performing. This fact has lead us to consider the problem of communicating modules (task implementations) in a large and structured knowledge based system when modules have different uncertainty calculi. In this paper, the analysis of the communication problem is made assuming that (i) each uncertainty calculus is an inference mechanism defining an entailment relation, and therefore the communication is considered to be inference-preserving, and (ii) we restrict ourselves to the case which the different uncertainty calculi are given by a class of truth functional Multiple-valued Logics.

A Symbolic Approach to Reasoning with Linguistic Quantifiers

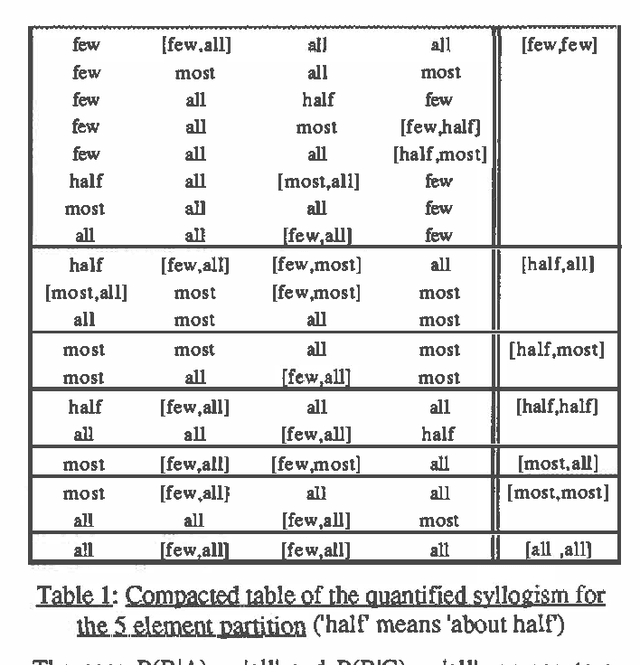
This paper investigates the possibility of performing automated reasoning in probabilistic logic when probabilities are expressed by means of linguistic quantifiers. Each linguistic term is expressed as a prescribed interval of proportions. Then instead of propagating numbers, qualitative terms are propagated in accordance with the numerical interpretation of these terms. The quantified syllogism, modelling the chaining of probabilistic rules, is studied in this context. It is shown that a qualitative counterpart of this syllogism makes sense, and is relatively independent of the threshold defining the linguistically meaningful intervals, provided that these threshold values remain in accordance with the intuition. The inference power is less than that of a full-fledged probabilistic con-quaint propagation device but better corresponds to what could be thought of as commonsense probabilistic reasoning.

On Modal Logics for Qualitative Possibility in a Fuzzy Setting

Within the possibilistic approach to uncertainty modeling, the paper presents a modal logical system to reason about qualitative (comparative) statements of the possibility (and necessity) of fuzzy propositions. We relate this qualitative modal logic to the many--valued analogues MVS5 and MVKD45 of the well known modal logics of knowledge and belief S5 and KD45 respectively. Completeness results are obtained for such logics and therefore, they extend previous existing results for qualitative possibilistic logics in the classical non-fuzzy setting.

Fuzzy Logic and Probability

In this paper we deal with a new approach to probabilistic reasoning in a logical framework. Nearly almost all logics of probability that have been proposed in the literature are based on classical two-valued logic. After making clear the differences between fuzzy logic and probability theory, here we propose a {em fuzzy} logic of probability for which completeness results (in a probabilistic sense) are provided. The main idea behind this approach is that probability values of crisp propositions can be understood as truth-values of some suitable fuzzy propositions associated to the crisp ones. Moreover, suggestions and examples of how to extend the formalism to cope with conditional probabilities and with other uncertainty formalisms are also provided.

On the Semantics and Automated Deduction for PLFC, a Logic of Possibilistic Uncertainty and Fuzziness

Possibilistic logic is a well-known graded logic of uncertainty suitable to reason under incomplete information and partially inconsistent knowledge, which is built upon classical first order logic. There exists for Possibilistic logic a proof procedure based on a refutation complete resolution-style calculus. Recently, a syntactical extension of first order Possibilistic logic (called PLFC) dealing with fuzzy constants and fuzzily restricted quantifiers has been proposed. Our aim is to present steps towards both the formalization of PLFC itself and an automated deduction system for it by (i) providing a formal semantics; (ii) defining a sound resolution-style calculus by refutation; and (iii) describing a first-order proof procedure for PLFC clauses based on (ii) and on a novel notion of most general substitution of two literals in a resolution step. In contrast to standard Possibilistic logic semantics, truth-evaluation of formulas with fuzzy constants are many-valued instead of boolean, and consequently an extended notion of possibilistic uncertainty is also needed.

A Complete Calculus for Possibilistic Logic Programming with Fuzzy Propositional Variables

In this paper we present a propositional logic programming language for reasoning under possibilistic uncertainty and representing vague knowledge. Formulas are represented by pairs (A, c), where A is a many-valued proposition and c is value in the unit interval [0,1] which denotes a lower bound on the belief on A in terms of necessity measures. Belief states are modeled by possibility distributions on the set of all many-valued interpretations. In this framework, (i) we define a syntax and a semantics of the general underlying uncertainty logic; (ii) we provide a modus ponens-style calculus for a sublanguage of Horn-rules and we prove that it is complete for determining the maximum degree of possibilistic belief with which a fuzzy propositional variable can be entailed from a set of formulas; and finally, (iii) we show how the computation of a partial matching between fuzzy propositional variables, in terms of necessity measures for fuzzy sets, can be included in our logic programming system.

A Logic Programming Framework for Possibilistic Argumentation with Vague Knowledge

Defeasible argumentation frameworks have evolved to become a sound setting to formalize commonsense, qualitative reasoning from incomplete and potentially inconsistent knowledge. Defeasible Logic Programming (DeLP) is a defeasible argumentation formalism based on an extension of logic programming. Although DeLP has been successfully integrated in a number of different real-world applications, DeLP cannot deal with explicit uncertainty, nor with vague knowledge, as defeasibility is directly encoded in the object language. This paper introduces P-DeLP, a new logic programming language that extends original DeLP capabilities for qualitative reasoning by incorporating the treatment of possibilistic uncertainty and fuzzy knowledge. Such features will be formalized on the basis of PGL, a possibilistic logic based on Godel fuzzy logic.