Belief revision and 3-valued logics: Characterization of 19,683 belief change operators

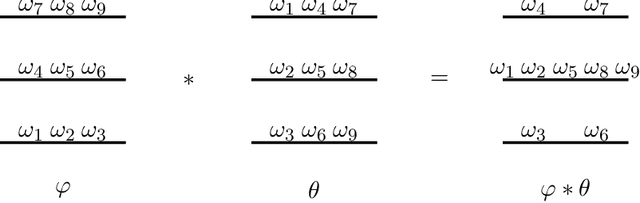
In most classical models of belief change, epistemic states are represented by theories (AGM) or formulas (Katsuno-Mendelzon) and the new pieces of information by formulas. The Representation Theorem for revision operators says that operators are represented by total preorders. This important representation is exploited by Darwiche and Pearl to shift the notion of epistemic state to a more abstract one, where the paradigm of epistemic state is indeed that of a total preorder over interpretations. In this work, we introduce a 3-valued logic where the formulas can be identified with a generalisation of total preorders of three levels: a ranking function mapping interpretations into the truth values. Then we analyse some sort of changes in this kind of structures and give syntactical characterizations of them.

Morphologic for knowledge dynamics: revision, fusion, abduction

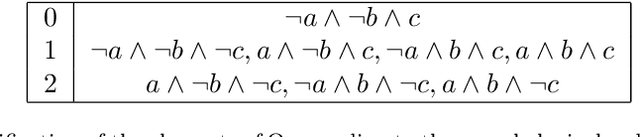
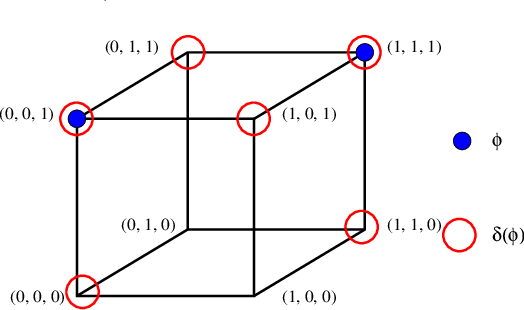
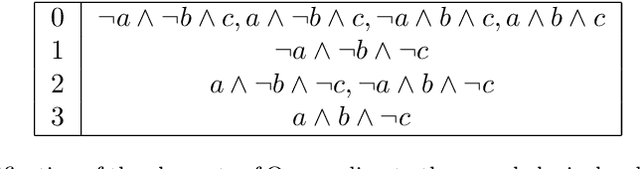
Several tasks in artificial intelligence require to be able to find models about knowledge dynamics. They include belief revision, fusion and belief merging, and abduction. In this paper we exploit the algebraic framework of mathematical morphology in the context of propositional logic, and define operations such as dilation or erosion of a set of formulas. We derive concrete operators, based on a semantic approach, that have an intuitive interpretation and that are formally well behaved, to perform revision, fusion and abduction. Computation and tractability are addressed, and simple examples illustrate the typical results that can be obtained.

Impossibility in Belief Merging

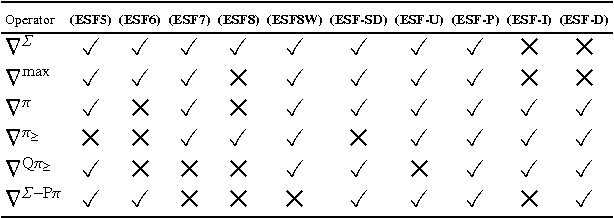
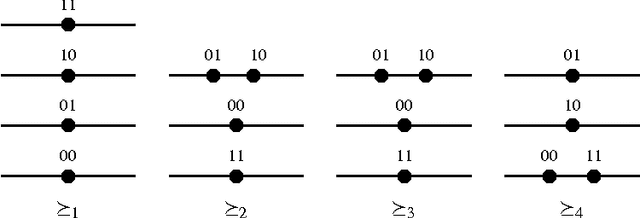
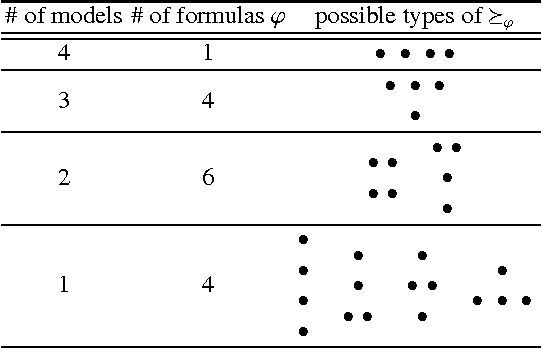
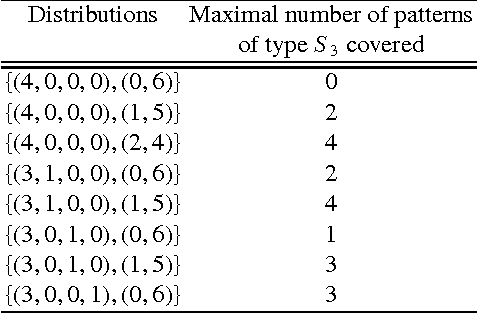
With the aim of studying social properties of belief merging and having a better understanding of impossibility, we extend in three ways the framework of logic-based merging introduced by Konieczny and Pino P\'erez. First, at the level of representation of the information, we pass from belief bases to complex epistemic states. Second, the profiles are represented as functions of finite societies to the set of epistemic states (a sort of vectors) and not as multisets of epistemic states. Third, we extend the set of rational postulates in order to consider the epistemic versions of the classical postulates of Social Choice Theory: Standard Domain, Pareto Property, Independence of Irrelevant Alternatives and Absence of Dictator. These epistemic versions of social postulates are given, essentially, in terms of the finite propositional logic. We state some representation theorems for these operators. These extensions and representation theorems allow us to establish an epistemic and very general version of Arrow's Impossibility Theorem. One of the interesting features of our result, is that it holds for different representations of epistemic states; for instance conditionals, Ordinal Conditional functions and, of course, total preorders.

Exploring the rationality of some syntactic merging operators (extended version)

Most merging operators are defined by semantics methods which have very high computational complexity. In order to have operators with a lower computational complexity, some merging operators defined in a syntactical way have be proposed. In this work we define some syntactical merging operators and exploring its rationality properties. To do that we constrain the belief bases to be sets of formulas very close to logic programs and the underlying logic is defined through forward chaining rule (Modus Ponens). We propose two types of operators: arbitration operators when the inputs are only two bases and fusion with integrity constraints operators. We introduce a set of postulates inspired of postulates LS, proposed by Liberatore and Shaerf and then we analyzed the first class of operators through these postulates. We also introduce a set of postulates inspired of postulates KP, proposed by Konieczny and Pino P\'erez and then we analyzed the second class of operators through these postulates.