Amílcar Mata Díaz
Impossibility in Belief Merging
Jun 14, 2016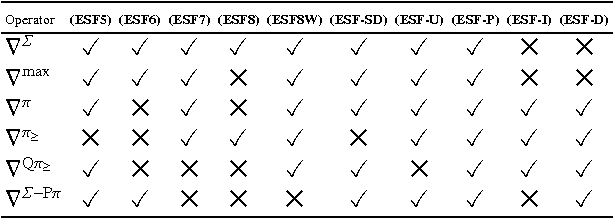
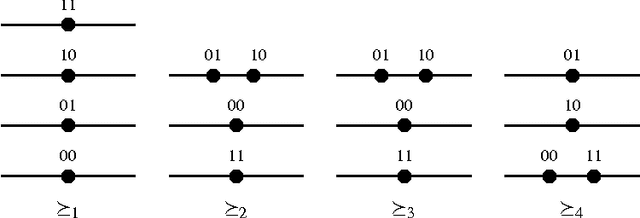
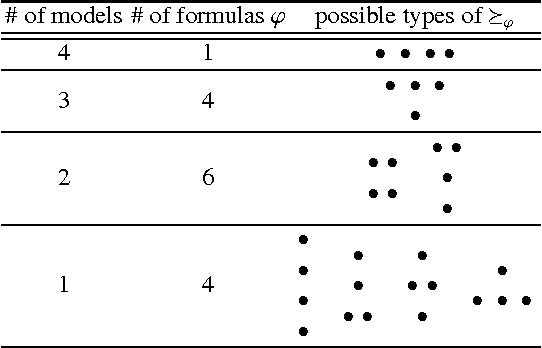
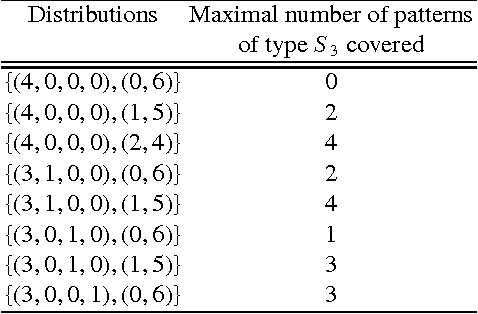
Abstract:With the aim of studying social properties of belief merging and having a better understanding of impossibility, we extend in three ways the framework of logic-based merging introduced by Konieczny and Pino P\'erez. First, at the level of representation of the information, we pass from belief bases to complex epistemic states. Second, the profiles are represented as functions of finite societies to the set of epistemic states (a sort of vectors) and not as multisets of epistemic states. Third, we extend the set of rational postulates in order to consider the epistemic versions of the classical postulates of Social Choice Theory: Standard Domain, Pareto Property, Independence of Irrelevant Alternatives and Absence of Dictator. These epistemic versions of social postulates are given, essentially, in terms of the finite propositional logic. We state some representation theorems for these operators. These extensions and representation theorems allow us to establish an epistemic and very general version of Arrow's Impossibility Theorem. One of the interesting features of our result, is that it holds for different representations of epistemic states; for instance conditionals, Ordinal Conditional functions and, of course, total preorders.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge