Simplified Kripke semantics for K45-like Godel modal logics and its axiomatic extensions

In this paper, we provide simplified semantics for the logic K45(G), i.e. the many-valued Godel counterpart of the classical modal logic K45. More precisely, we characterize K45(G) as the set of valid formulae of the class of possibilistic Godel Kripke Frames <W,\pi> where W is a non-empty set of worlds and \pi: W \to [0, 1] is a possibility distribution on W.

Logics of formal inconsistency arising from systems of fuzzy logic

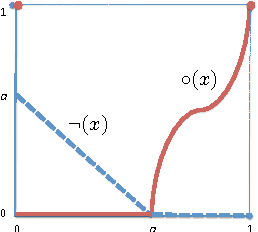
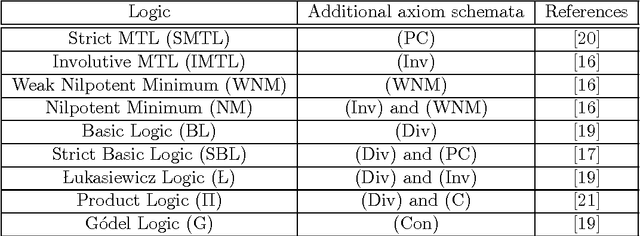
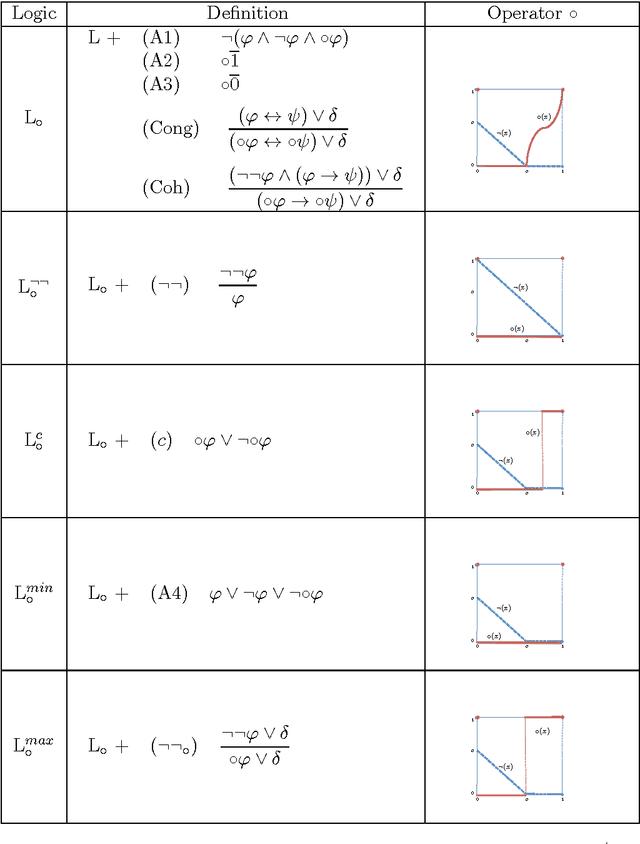
This paper proposes the meeting of fuzzy logic with paraconsistency in a very precise and foundational way. Specifically, in this paper we introduce expansions of the fuzzy logic MTL by means of primitive operators for consistency and inconsistency in the style of the so-called Logics of Formal Inconsistency (LFIs). The main novelty of the present approach is the definition of postulates for this type of operators over MTL-algebras, leading to the definition and axiomatization of a family of logics, expansions of MTL, whose degree-preserving counterpart are paraconsistent and moreover LFIs.

Combining Multiple-Valued Logics in Modular Expert Systems

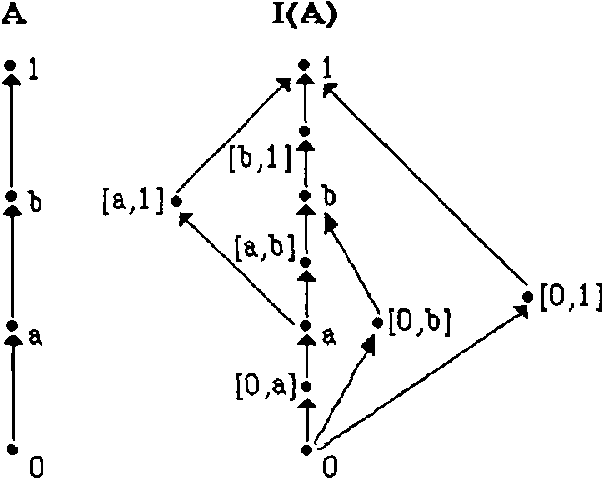
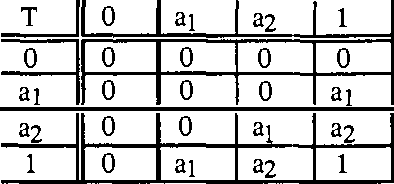
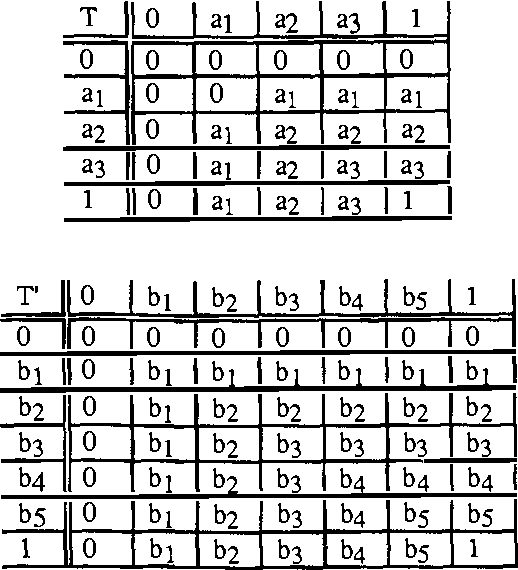
The way experts manage uncertainty usually changes depending on the task they are performing. This fact has lead us to consider the problem of communicating modules (task implementations) in a large and structured knowledge based system when modules have different uncertainty calculi. In this paper, the analysis of the communication problem is made assuming that (i) each uncertainty calculus is an inference mechanism defining an entailment relation, and therefore the communication is considered to be inference-preserving, and (ii) we restrict ourselves to the case which the different uncertainty calculi are given by a class of truth functional Multiple-valued Logics.

On Modal Logics for Qualitative Possibility in a Fuzzy Setting

Within the possibilistic approach to uncertainty modeling, the paper presents a modal logical system to reason about qualitative (comparative) statements of the possibility (and necessity) of fuzzy propositions. We relate this qualitative modal logic to the many--valued analogues MVS5 and MVKD45 of the well known modal logics of knowledge and belief S5 and KD45 respectively. Completeness results are obtained for such logics and therefore, they extend previous existing results for qualitative possibilistic logics in the classical non-fuzzy setting.

Fuzzy Logic and Probability

In this paper we deal with a new approach to probabilistic reasoning in a logical framework. Nearly almost all logics of probability that have been proposed in the literature are based on classical two-valued logic. After making clear the differences between fuzzy logic and probability theory, here we propose a {em fuzzy} logic of probability for which completeness results (in a probabilistic sense) are provided. The main idea behind this approach is that probability values of crisp propositions can be understood as truth-values of some suitable fuzzy propositions associated to the crisp ones. Moreover, suggestions and examples of how to extend the formalism to cope with conditional probabilities and with other uncertainty formalisms are also provided.