Optical images-based edge detection in Synthetic Aperture Radar images

We address the issue of adapting optical images-based edge detection techniques for use in Polarimetric Synthetic Aperture Radar (PolSAR) imagery. We modify the gravitational edge detection technique (inspired by the Law of Universal Gravity) proposed by Lopez-Molina et al, using the non-standard neighbourhood configuration proposed by Fu et al, to reduce the speckle noise in polarimetric SAR imagery. We compare the modified and unmodified versions of the gravitational edge detection technique with the well-established one proposed by Canny, as well as with a recent multiscale fuzzy-based technique proposed by Lopez-Molina et Alejandro We also address the issues of aggregation of gray level images before and after edge detection and of filtering. All techniques addressed here are applied to a mosaic built using class distributions obtained from a real scene, as well as to the true PolSAR image; the mosaic results are assessed using Baddeley's Delta Metric. Our experiments show that modifying the gravitational edge detection technique with a non-standard neighbourhood configuration produces better results than the original technique, as well as the other techniques used for comparison. The experiments show that adapting edge detection methods from Computational Intelligence for use in PolSAR imagery is a new field worthy of exploration.

Structuring Bodies of Evidence

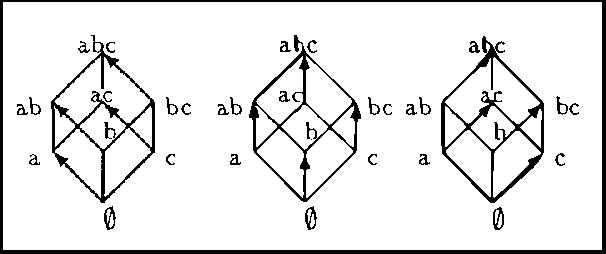
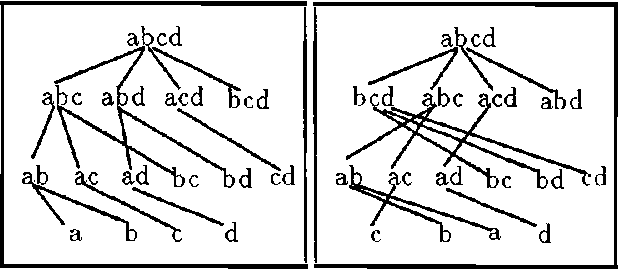
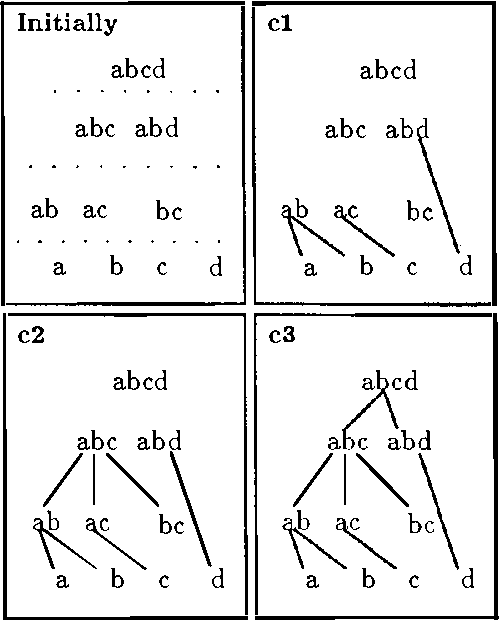
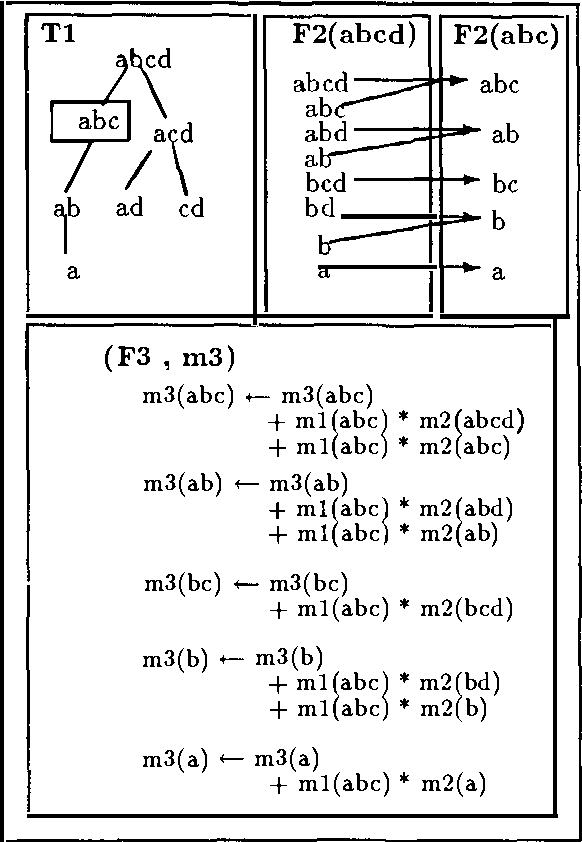
In this article we present two ways of structuring bodies of evidence, which allow us to reduce the complexity of the operations usually performed in the framework of evidence theory. The first structure just partitions the focal elements in a body of evidence by their cardinality. With this structure we are able to reduce the complexity on the calculation of the belief functions Bel, Pl, and Q. The other structure proposed here, the Hierarchical Trees, permits us to reduce the complexity of the calculation of Bel, Pl, and Q, as well as of the Dempster's rule of combination in relation to the brute-force algorithm. Both these structures do not require the generation of all the subsets of the reference domain.

On the Semantics and Automated Deduction for PLFC, a Logic of Possibilistic Uncertainty and Fuzziness

Possibilistic logic is a well-known graded logic of uncertainty suitable to reason under incomplete information and partially inconsistent knowledge, which is built upon classical first order logic. There exists for Possibilistic logic a proof procedure based on a refutation complete resolution-style calculus. Recently, a syntactical extension of first order Possibilistic logic (called PLFC) dealing with fuzzy constants and fuzzily restricted quantifiers has been proposed. Our aim is to present steps towards both the formalization of PLFC itself and an automated deduction system for it by (i) providing a formal semantics; (ii) defining a sound resolution-style calculus by refutation; and (iii) describing a first-order proof procedure for PLFC clauses based on (ii) and on a novel notion of most general substitution of two literals in a resolution step. In contrast to standard Possibilistic logic semantics, truth-evaluation of formulas with fuzzy constants are many-valued instead of boolean, and consequently an extended notion of possibilistic uncertainty is also needed.