On the Complexity of Decision Making in Possibilistic Decision Trees
Paper and Code
Feb 14, 2012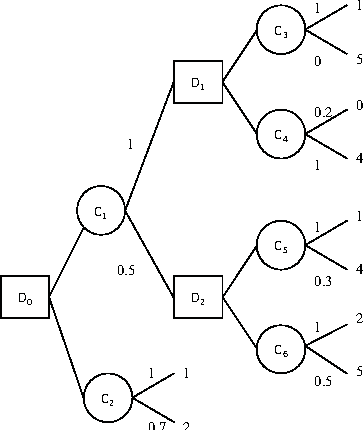
When the information about uncertainty cannot be quantified in a simple, probabilistic way, the topic of possibilistic decision theory is often a natural one to consider. The development of possibilistic decision theory has lead to a series of possibilistic criteria, e.g pessimistic possibilistic qualitative utility, possibilistic likely dominance, binary possibilistic utility and possibilistic Choquet integrals. This paper focuses on sequential decision making in possibilistic decision trees. It proposes a complexity study of the problem of finding an optimal strategy depending on the monotonicity property of the optimization criteria which allows the application of dynamic programming that offers a polytime reduction of the decision problem. It also shows that possibilistic Choquet integrals do not satisfy this property, and that in this case the optimization problem is NP - hard.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge