Nahla Ben Amor
LARODEC
Possibilistic Networks: Parameters Learning from Imprecise Data and Evaluation strategy
Jul 13, 2016Abstract:There has been an ever-increasing interest in multidisciplinary research on representing and reasoning with imperfect data. Possibilistic networks present one of the powerful frameworks of interest for representing uncertain and imprecise information. This paper covers the problem of their parameters learning from imprecise datasets, i.e., containing multi-valued data. We propose in the rst part of this paper a possibilistic networks sampling process. In the second part, we propose a likelihood function which explores the link between random sets theory and possibility theory. This function is then deployed to parametrize possibilistic networks.
Compiling Possibilistic Networks: Alternative Approaches to Possibilistic Inference
Mar 15, 2012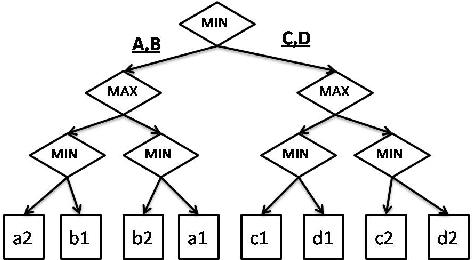
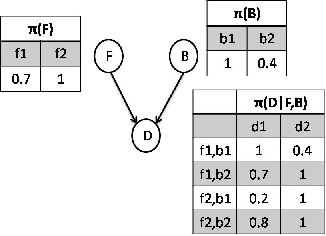
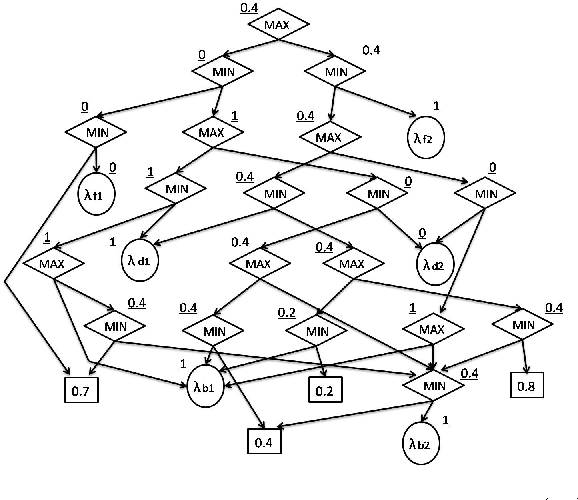
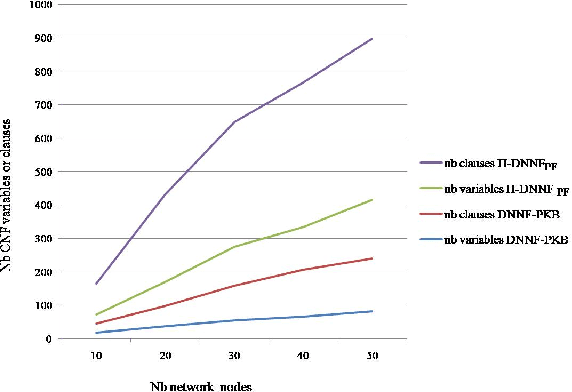
Abstract:Qualitative possibilistic networks, also known as min-based possibilistic networks, are important tools for handling uncertain information in the possibility theory frame- work. Despite their importance, only the junction tree adaptation has been proposed for exact reasoning with such networks. This paper explores alternative algorithms using compilation techniques. We first propose possibilistic adaptations of standard compilation-based probabilistic methods. Then, we develop a new, purely possibilistic, method based on the transformation of the initial network into a possibilistic base. A comparative study shows that this latter performs better than the possibilistic adap- tations of probabilistic methods. This result is also confirmed by experimental results.
On the Complexity of Decision Making in Possibilistic Decision Trees
Feb 14, 2012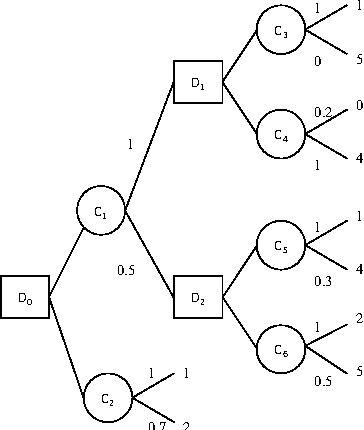
Abstract:When the information about uncertainty cannot be quantified in a simple, probabilistic way, the topic of possibilistic decision theory is often a natural one to consider. The development of possibilistic decision theory has lead to a series of possibilistic criteria, e.g pessimistic possibilistic qualitative utility, possibilistic likely dominance, binary possibilistic utility and possibilistic Choquet integrals. This paper focuses on sequential decision making in possibilistic decision trees. It proposes a complexity study of the problem of finding an optimal strategy depending on the monotonicity property of the optimization criteria which allows the application of dynamic programming that offers a polytime reduction of the decision problem. It also shows that possibilistic Choquet integrals do not satisfy this property, and that in this case the optimization problem is NP - hard.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge