A General Modifier-based Framework for Inconsistency-Tolerant Query Answering

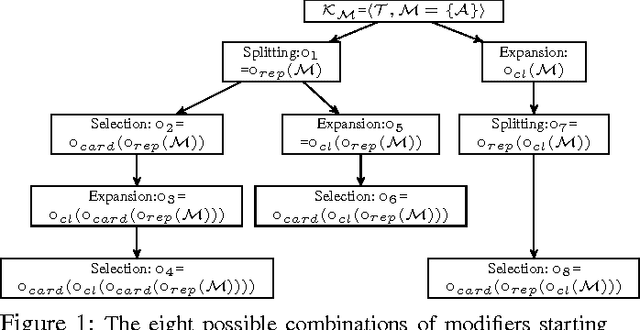
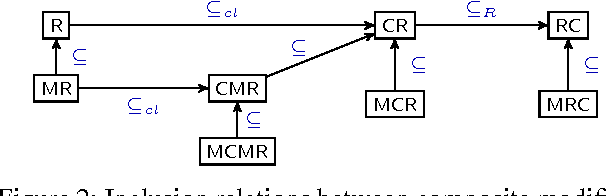
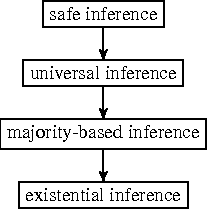
We propose a general framework for inconsistency-tolerant query answering within existential rule setting. This framework unifies the main semantics proposed by the state of art and introduces new ones based on cardinality and majority principles. It relies on two key notions: modifiers and inference strategies. An inconsistency-tolerant semantics is seen as a composite modifier plus an inference strategy. We compare the obtained semantics from a productivity point of view.

Argumentative inference in uncertain and inconsistent knowledge bases

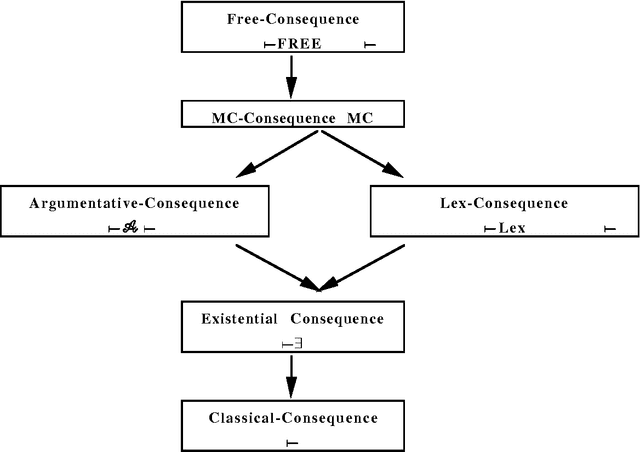
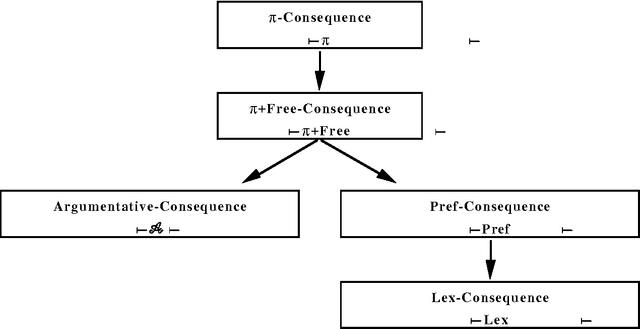
This paper presents and discusses several methods for reasoning from inconsistent knowledge bases. A so-called argumentative-consequence relation taking into account the existence of consistent arguments in favor of a conclusion and the absence of consistent arguments in favor of its contrary, is particularly investigated. Flat knowledge bases, i.e. without any priority between their elements, as well as prioritized ones where some elements are considered as more strongly entrenched than others are studied under different consequence relations. Lastly a paraconsistent-like treatment of prioritized knowledge bases is proposed, where both the level of entrenchment and the level of paraconsistency attached to a formula are propagated. The priority levels are handled in the framework of possibility theory.

Belief Functions and Default Reasoning

We present a new approach to dealing with default information based on the theory of belief functions. Our semantic structures, inspired by Adams' epsilon-semantics, are epsilon-belief assignments, where values committed to focal elements are either close to 0 or close to 1. We define two systems based on these structures, and relate them to other non-monotonic systems presented in the literature. We show that our second system correctly addresses the well-known problems of specificity, irrelevance, blocking of inheritance, ambiguity, and redundancy.

Coping with the Limitations of Rational Inference in the Framework of Possibility Theory

Possibility theory offers a framework where both Lehmann's "preferential inference" and the more productive (but less cautious) "rational closure inference" can be represented. However, there are situations where the second inference does not provide expected results either because it cannot produce them, or even provide counter-intuitive conclusions. This state of facts is not due to the principle of selecting a unique ordering of interpretations (which can be encoded by one possibility distribution), but rather to the absence of constraints expressing pieces of knowledge we have implicitly in mind. It is advocated in this paper that constraints induced by independence information can help finding the right ordering of interpretations. In particular, independence constraints can be systematically assumed with respect to formulas composed of literals which do not appear in the conditional knowledge base, or for default rules with respect to situations which are "normal" according to the other default rules in the base. The notion of independence which is used can be easily expressed in the qualitative setting of possibility theory. Moreover, when a counter-intuitive plausible conclusion of a set of defaults, is in its rational closure, but not in its preferential closure, it is always possible to repair the set of defaults so as to produce the desired conclusion.

Merging Uncertain Knowledge Bases in a Possibilistic Logic Framework

This paper addresses the problem of merging uncertain information in the framework of possibilistic logic. It presents several syntactic combination rules to merge possibilistic knowledge bases, provided by different sources, into a new possibilistic knowledge base. These combination rules are first described at the meta-level outside the language of possibilistic logic. Next, an extension of possibilistic logic, where the combination rules are inside the language, is proposed. A proof system in a sequent form, which is sound and complete with respect to the possibilistic logic semantics, is given.

Possibilistic logic bases and possibilistic graphs

Possibilistic logic bases and possibilistic graphs are two different frameworks of interest for representing knowledge. The former stratifies the pieces of knowledge (expressed by logical formulas) according to their level of certainty, while the latter exhibits relationships between variables. The two types of representations are semantically equivalent when they lead to the same possibility distribution (which rank-orders the possible interpretations). A possibility distribution can be decomposed using a chain rule which may be based on two different kinds of conditioning which exist in possibility theory (one based on product in a numerical setting, one based on minimum operation in a qualitative setting). These two types of conditioning induce two kinds of possibilistic graphs. In both cases, a translation of these graphs into possibilistic bases is provided. The converse translation from a possibilistic knowledge base into a min-based graph is also described.

A Principled Analysis of Merging Operations in Possibilistic Logic

Possibilistic logic offers a qualitative framework for representing pieces of information associated with levels of uncertainty of priority. The fusion of multiple sources information is discussed in this setting. Different classes of merging operators are considered including conjunctive, disjunctive, reinforcement, adaptive and averaging operators. Then we propose to analyse these classes in terms of postulates. This is done by first extending the postulate for merging classical bases to the case where priorites are avaialbe.

Graphical readings of possibilistic logic bases

Possibility theory offers either a qualitive, or a numerical framework for representing uncertainty, in terms of dual measures of possibility and necessity. This leads to the existence of two kinds of possibilistic causal graphs where the conditioning is either based on the minimum, or the product operator. Benferhat et al. (1999) have investigated the connections between min-based graphs and possibilistic logic bases (made of classical formulas weighted in terms of certainty). This paper deals with a more difficult issue : the product-based graphical representations of possibilistic bases, which provides an easy structural reading of possibilistic bases. Moreover, this paper also provides another reading of possibilistic bases in terms of comparative preferences of the form "in the context p, q is preferred to not q". This enables us to explicit preferences underlying a set of goals with different levels of priority.

Bipolar Possibilistic Representations

Recently, it has been emphasized that the possibility theory framework allows us to distinguish between i) what is possible because it is not ruled out by the available knowledge, and ii) what is possible for sure. This distinction may be useful when representing knowledge, for modelling values which are not impossible because they are consistent with the available knowledge on the one hand, and values guaranteed to be possible because reported from observations on the other hand. It is also of interest when expressing preferences, to point out values which are positively desired among those which are not rejected. This distinction can be encoded by two types of constraints expressed in terms of necessity measures and in terms of guaranteed possibility functions, which induce a pair of possibility distributions at the semantic level. A consistency condition should ensure that what is claimed to be guaranteed as possible is indeed not impossible. The present paper investigates the representation of this bipolar view, including the case when it is stated by means of conditional measures, or by means of comparative context-dependent constraints. The interest of this bipolar framework, which has been recently stressed for expressing preferences, is also pointed out in the representation of diagnostic knowledge.

A possibilistic handling of partially ordered information

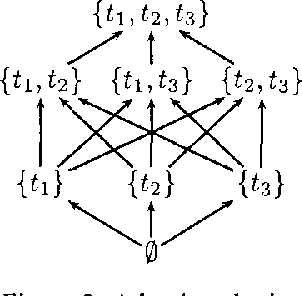
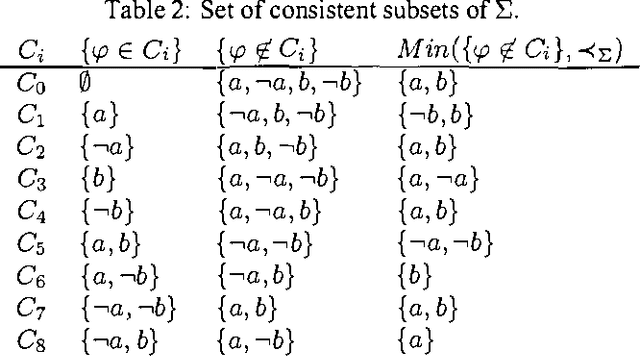
In a standard possibilistic logic, prioritized information are encoded by means of weighted knowledge base. This paper proposes an extension of possibilistic logic for dealing with partially ordered information. We Show that all basic notions of standard possibilitic logic (sumbsumption, syntactic and semantic inference, etc.) have natural couterparts when dealing with partially ordered information. We also propose an algorithm which computes possibilistic conclusions of a partial knowledge base of a partially ordered knowlege base.