Query Rewriting with Disjunctive Existential Rules and Mappings

We consider the issue of answering unions of conjunctive queries (UCQs) with disjunctive existential rules and mappings. While this issue has already been well studied from a chase perspective, query rewriting within UCQs has hardly been addressed yet. We first propose a sound and complete query rewriting operator, which has the advantage of establishing a tight relationship between a chase step and a rewriting step. The associated breadth-first query rewriting algorithm outputs a minimal UCQ-rewriting when one exists. Second, we show that for any ``truly disjunctive'' nonrecursive rule, there exists a conjunctive query that has no UCQ-rewriting. It follows that the notion of finite unification sets (fus), which denotes sets of existential rules such that any UCQ admits a UCQ-rewriting, seems to have little relevance in this setting. Finally, turning our attention to mappings, we show that the problem of determining whether a UCQ admits a UCQ-rewriting through a disjunctive mapping is undecidable. We conclude with a number of open problems.

Normalisations of Existential Rules: Not so Innocuous!

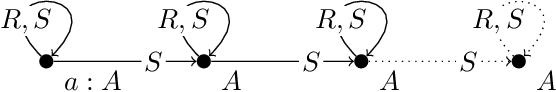
Existential rules are an expressive knowledge representation language mainly developed to query data. In the literature, they are often supposed to be in some normal form that simplifies technical developments. For instance, a common assumption is that rule heads are atomic, i.e., restricted to a single atom. Such assumptions are considered to be made without loss of generality as long as all sets of rules can be normalised while preserving entailment. However, an important question is whether the properties that ensure the decidability of reasoning are preserved as well. We provide a systematic study of the impact of these procedures on the different chase variants with respect to chase (non-)termination and FO-rewritability. This also leads us to study open problems related to chase termination of independent interest.

Parallelisable Existential Rules: a Story of Pieces

In this paper, we consider existential rules, an expressive formalism well suited to the representation of ontological knowledge and data-to-ontology mappings in the context of ontology-based data integration. The chase is a fundamental tool to do reasoning with existential rules as it computes all the facts entailed by the rules from a database instance. We introduce parallelisable sets of existential rules, for which the chase can be computed in a single breadth-first step from any instance. The question we investigate is the characterization of such rule sets. We show that parallelisable rule sets are exactly those rule sets both bounded for the chase and belonging to a novel class of rules, called pieceful. The pieceful class includes in particular frontier-guarded existential rules and (plain) datalog. We also give another characterization of parallelisable rule sets in terms of rule composition based on rewriting.

Oblivious and Semi-Oblivious Boundedness for Existential Rules

We study the notion of boundedness in the context of positive existential rules, that is, whether there exists an upper bound to the depth of the chase procedure, that is independent from the initial instance. By focussing our attention on the oblivious and the semi-oblivious chase variants, we give a characterization of boundedness in terms of FO-rewritability and chase termination. We show that it is decidable to recognize if a set of rules is bounded for several classes and outline the complexity of the problem. This report contains the paper published at IJCAI 2019 and an appendix with full proofs.

Characterizing Boundedness in Chase Variants

Existential rules are a positive fragment of first-order logic that generalizes function-free Horn rules by allowing existentially quantified variables in rule heads. This family of languages has recently attracted significant interest in the context of ontology-mediated query answering. Forward chaining, also known as the chase, is a fundamental tool for computing universal models of knowledge bases, which consist of existential rules and facts. Several chase variants have been defined, which differ on the way they handle redundancies. A set of existential rules is bounded if it ensures the existence of a bound on the depth of the chase, independently from any set of facts. Deciding if a set of rules is bounded is an undecidable problem for all chase variants. Nevertheless, when computing universal models, knowing that a set of rules is bounded for some chase variant does not help much in practice if the bound remains unknown or even very large. Hence, we investigate the decidability of the k-boundedness problem, which asks whether the depth of the chase for a given set of rules is bounded by an integer k. We identify a general property which, when satisfied by a chase variant, leads to the decidability of k-boundedness. We then show that the main chase variants satisfy this property, namely the oblivious, semi-oblivious (aka Skolem), and restricted chase, as well as their breadth-first versions. This paper is under consideration for publication in Theory and Practice of Logic Programming.

On the k-Boundedness for Existential Rules

The chase is a fundamental tool for existential rules. Several chase variants are known, which differ on how they handle redundancies possibly caused by the introduction of nulls. Given a chase variant, the halting problem takes as input a set of existential rules and asks if this set of rules ensures the termination of the chase for any factbase. It is well-known that this problem is undecidable for all known chase variants. The related problem of boundedness asks if a given set of existential rules is bounded, i.e., whether there is a predefined upper bound on the number of (breadth-first) steps of the chase, independently from any factbase. This problem is already undecidable in the specific case of datalog rules. However, knowing that a set of rules is bounded for some chase variant does not help much in practice if the bound is unknown. Hence, in this paper, we investigate the decidability of the k-boundedness problem, which asks whether a given set of rules is bounded by an integer k. We prove that k-boundedness is decidable for three chase variants, namely the oblivious, semi-oblivious and restricted chase.

Combining Existential Rules and Transitivity: Next Steps

We consider existential rules (aka Datalog+) as a formalism for specifying ontologies. In recent years, many classes of existential rules have been exhibited for which conjunctive query (CQ) entailment is decidable. However, most of these classes cannot express transitivity of binary relations, a frequently used modelling construct. In this paper, we address the issue of whether transitivity can be safely combined with decidable classes of existential rules. First, we prove that transitivity is incompatible with one of the simplest decidable classes, namely aGRD (acyclic graph of rule dependencies), which clarifies the landscape of `finite expansion sets' of rules. Second, we show that transitivity can be safely added to linear rules (a subclass of guarded rules, which generalizes the description logic DL-Lite-R) in the case of atomic CQs, and also for general CQs if we place a minor syntactic restriction on the rule set. This is shown by means of a novel query rewriting algorithm that is specially tailored to handle transitivity rules. Third, for the identified decidable cases, we pinpoint the combined and data complexities of query entailment.

A General Modifier-based Framework for Inconsistency-Tolerant Query Answering

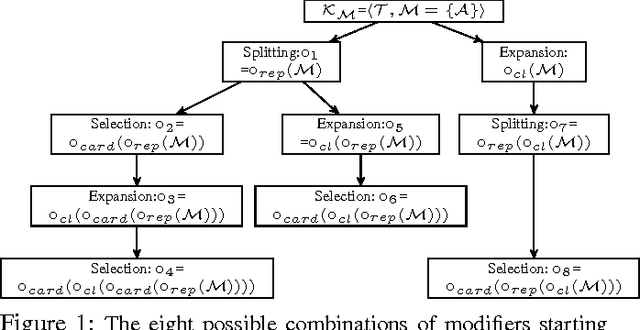
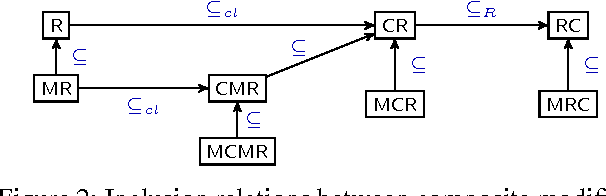
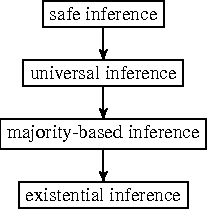
We propose a general framework for inconsistency-tolerant query answering within existential rule setting. This framework unifies the main semantics proposed by the state of art and introduces new ones based on cardinality and majority principles. It relies on two key notions: modifiers and inference strategies. An inconsistency-tolerant semantics is seen as a composite modifier plus an inference strategy. We compare the obtained semantics from a productivity point of view.

Worst-case Optimal Query Answering for Greedy Sets of Existential Rules and Their Subclasses

The need for an ontological layer on top of data, associated with advanced reasoning mechanisms able to exploit the semantics encoded in ontologies, has been acknowledged both in the database and knowledge representation communities. We focus in this paper on the ontological query answering problem, which consists of querying data while taking ontological knowledge into account. More specifically, we establish complexities of the conjunctive query entailment problem for classes of existential rules (also called tuple-generating dependencies, Datalog+/- rules, or forall-exists-rules. Our contribution is twofold. First, we introduce the class of greedy bounded-treewidth sets (gbts) of rules, which covers guarded rules, and their most well-known generalizations. We provide a generic algorithm for query entailment under gbts, which is worst-case optimal for combined complexity with or without bounded predicate arity, as well as for data complexity and query complexity. Secondly, we classify several gbts classes, whose complexity was unknown, with respect to combined complexity (with both unbounded and bounded predicate arity) and data complexity to obtain a comprehensive picture of the complexity of existential rule fragments that are based on diverse guardedness notions. Upper bounds are provided by showing that the proposed algorithm is optimal for all of them.

Extending Acyclicity Notions for Existential Rules (\emph{long version})

Existential rules have been proposed for representing ontological knowledge, specifically in the context of Ontology-Based Query Answering. Entailment with existential rules is undecidable. We focus in this paper on conditions that ensure the termination of a breadth-first forward chaining algorithm known as the chase. First, we propose a new tool that allows to extend existing acyclicity conditions ensuring chase termination, while keeping good complexity properties. Second, we consider the extension to existential rules with nonmonotonic negation under stable model semantics and further extend acyclicity results obtained in the positive case.