Query Rewriting with Disjunctive Existential Rules and Mappings

We consider the issue of answering unions of conjunctive queries (UCQs) with disjunctive existential rules and mappings. While this issue has already been well studied from a chase perspective, query rewriting within UCQs has hardly been addressed yet. We first propose a sound and complete query rewriting operator, which has the advantage of establishing a tight relationship between a chase step and a rewriting step. The associated breadth-first query rewriting algorithm outputs a minimal UCQ-rewriting when one exists. Second, we show that for any ``truly disjunctive'' nonrecursive rule, there exists a conjunctive query that has no UCQ-rewriting. It follows that the notion of finite unification sets (fus), which denotes sets of existential rules such that any UCQ admits a UCQ-rewriting, seems to have little relevance in this setting. Finally, turning our attention to mappings, we show that the problem of determining whether a UCQ admits a UCQ-rewriting through a disjunctive mapping is undecidable. We conclude with a number of open problems.

Oblivious and Semi-Oblivious Boundedness for Existential Rules

We study the notion of boundedness in the context of positive existential rules, that is, whether there exists an upper bound to the depth of the chase procedure, that is independent from the initial instance. By focussing our attention on the oblivious and the semi-oblivious chase variants, we give a characterization of boundedness in terms of FO-rewritability and chase termination. We show that it is decidable to recognize if a set of rules is bounded for several classes and outline the complexity of the problem. This report contains the paper published at IJCAI 2019 and an appendix with full proofs.

Characterizing Boundedness in Chase Variants

Existential rules are a positive fragment of first-order logic that generalizes function-free Horn rules by allowing existentially quantified variables in rule heads. This family of languages has recently attracted significant interest in the context of ontology-mediated query answering. Forward chaining, also known as the chase, is a fundamental tool for computing universal models of knowledge bases, which consist of existential rules and facts. Several chase variants have been defined, which differ on the way they handle redundancies. A set of existential rules is bounded if it ensures the existence of a bound on the depth of the chase, independently from any set of facts. Deciding if a set of rules is bounded is an undecidable problem for all chase variants. Nevertheless, when computing universal models, knowing that a set of rules is bounded for some chase variant does not help much in practice if the bound remains unknown or even very large. Hence, we investigate the decidability of the k-boundedness problem, which asks whether the depth of the chase for a given set of rules is bounded by an integer k. We identify a general property which, when satisfied by a chase variant, leads to the decidability of k-boundedness. We then show that the main chase variants satisfy this property, namely the oblivious, semi-oblivious (aka Skolem), and restricted chase, as well as their breadth-first versions. This paper is under consideration for publication in Theory and Practice of Logic Programming.

Sound, Complete and Minimal UCQ-Rewriting for Existential Rules

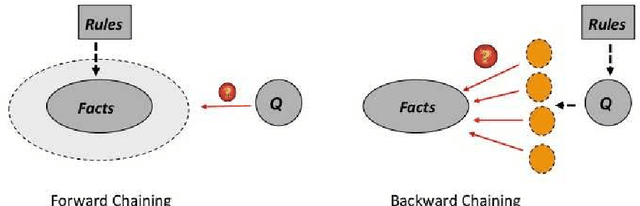
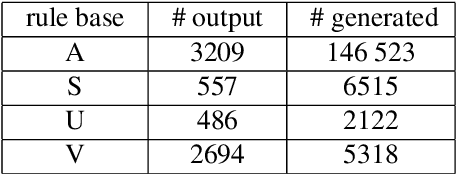
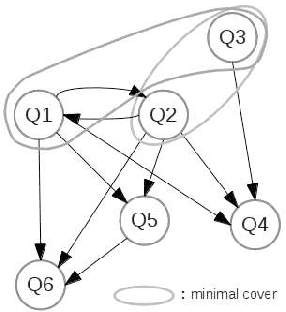
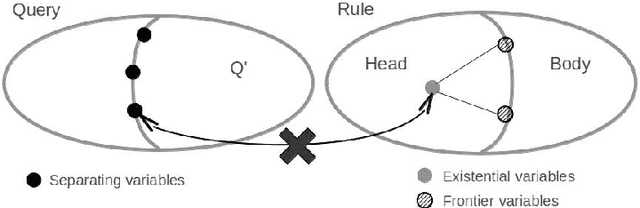
We address the issue of Ontology-Based Data Access, with ontologies represented in the framework of existential rules, also known as Datalog+/-. A well-known approach involves rewriting the query using ontological knowledge. We focus here on the basic rewriting technique which consists of rewriting the initial query into a union of conjunctive queries. First, we study a generic breadth-first rewriting algorithm, which takes as input any rewriting operator, and define properties of rewriting operators that ensure the correctness of the algorithm. Then, we focus on piece-unifiers, which provide a rewriting operator with the desired properties. Finally, we propose an implementation of this framework and report some experiments.