Normalisations of Existential Rules: Not so Innocuous!

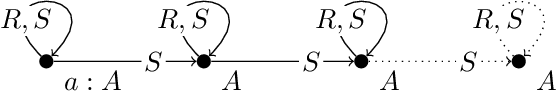
Existential rules are an expressive knowledge representation language mainly developed to query data. In the literature, they are often supposed to be in some normal form that simplifies technical developments. For instance, a common assumption is that rule heads are atomic, i.e., restricted to a single atom. Such assumptions are considered to be made without loss of generality as long as all sets of rules can be normalised while preserving entailment. However, an important question is whether the properties that ensure the decidability of reasoning are preserved as well. We provide a systematic study of the impact of these procedures on the different chase variants with respect to chase (non-)termination and FO-rewritability. This also leads us to study open problems related to chase termination of independent interest.

Parallelisable Existential Rules: a Story of Pieces

In this paper, we consider existential rules, an expressive formalism well suited to the representation of ontological knowledge and data-to-ontology mappings in the context of ontology-based data integration. The chase is a fundamental tool to do reasoning with existential rules as it computes all the facts entailed by the rules from a database instance. We introduce parallelisable sets of existential rules, for which the chase can be computed in a single breadth-first step from any instance. The question we investigate is the characterization of such rule sets. We show that parallelisable rule sets are exactly those rule sets both bounded for the chase and belonging to a novel class of rules, called pieceful. The pieceful class includes in particular frontier-guarded existential rules and (plain) datalog. We also give another characterization of parallelisable rule sets in terms of rule composition based on rewriting.

Answering Counting Queries over DL-Lite Ontologies

Ontology-mediated query answering (OMQA) is a promising approach to data access and integration that has been actively studied in the knowledge representation and database communities for more than a decade. The vast majority of work on OMQA focuses on conjunctive queries, whereas more expressive queries that feature counting or other forms of aggregation remain largely unex-plored. In this paper, we introduce a general form of counting query, relate it to previous proposals, and study the complexity of answering such queries in the presence of DL-Lite ontologies. As it follows from existing work that query answering is intractable and often of high complexity, we consider some practically relevant restrictions, for which we establish improved complexity bounds.

Reasoning about disclosure in data integration in the presence of source constraints

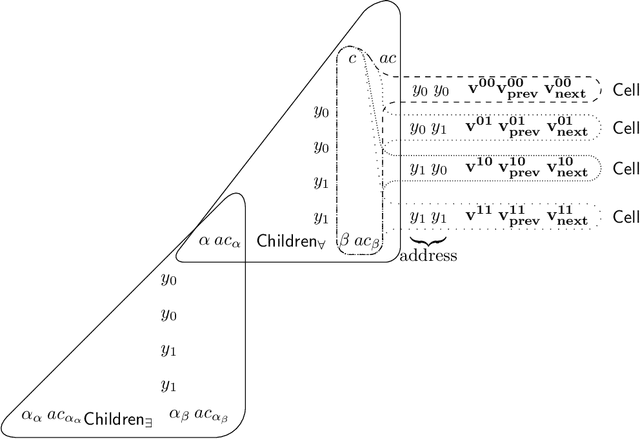
Data integration systems allow users to access data sitting in multiple sources by means of queries over a global schema, related to the sources via mappings. Data sources often contain sensitive information, and thus an analysis is needed to verify that a schema satisfies a privacy policy, given as a set of queries whose answers should not be accessible to users. Such an analysis should take into account not only knowledge that an attacker may have about the mappings, but also what they may know about the semantics of the sources. In this paper, we show that source constraints can have a dramatic impact on disclosure analysis. We study the problem of determining whether a given data integration system discloses a source query to an attacker in the presence of constraints, providing both lower and upper bounds on source-aware disclosure analysis.

Worst-case Optimal Query Answering for Greedy Sets of Existential Rules and Their Subclasses

The need for an ontological layer on top of data, associated with advanced reasoning mechanisms able to exploit the semantics encoded in ontologies, has been acknowledged both in the database and knowledge representation communities. We focus in this paper on the ontological query answering problem, which consists of querying data while taking ontological knowledge into account. More specifically, we establish complexities of the conjunctive query entailment problem for classes of existential rules (also called tuple-generating dependencies, Datalog+/- rules, or forall-exists-rules. Our contribution is twofold. First, we introduce the class of greedy bounded-treewidth sets (gbts) of rules, which covers guarded rules, and their most well-known generalizations. We provide a generic algorithm for query entailment under gbts, which is worst-case optimal for combined complexity with or without bounded predicate arity, as well as for data complexity and query complexity. Secondly, we classify several gbts classes, whose complexity was unknown, with respect to combined complexity (with both unbounded and bounded predicate arity) and data complexity to obtain a comprehensive picture of the complexity of existential rule fragments that are based on diverse guardedness notions. Upper bounds are provided by showing that the proposed algorithm is optimal for all of them.

Sound, Complete and Minimal UCQ-Rewriting for Existential Rules

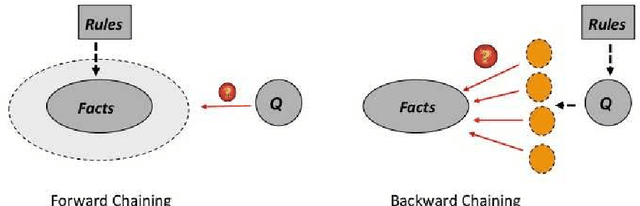
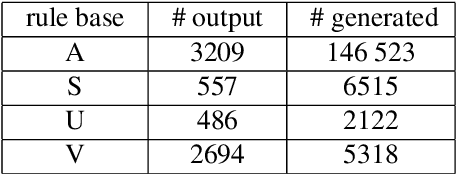
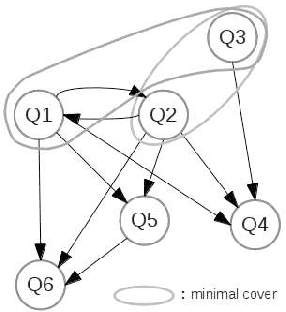
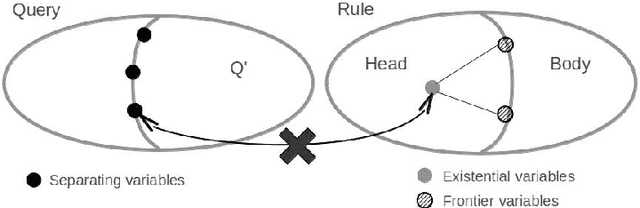
We address the issue of Ontology-Based Data Access, with ontologies represented in the framework of existential rules, also known as Datalog+/-. A well-known approach involves rewriting the query using ontological knowledge. We focus here on the basic rewriting technique which consists of rewriting the initial query into a union of conjunctive queries. First, we study a generic breadth-first rewriting algorithm, which takes as input any rewriting operator, and define properties of rewriting operators that ensure the correctness of the algorithm. Then, we focus on piece-unifiers, which provide a rewriting operator with the desired properties. Finally, we propose an implementation of this framework and report some experiments.